题目内容
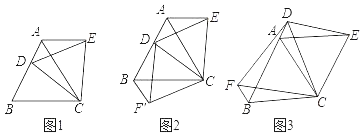
【题目】（1）如图1，D是等边三角形ABC边BA上一动点（点D）与点B不重合，连接CD，以CD为边在BC上方作等边三角形DCE，连接AE，你能发现AE与BD之间的数量关系吗？并证明你发现的结论．
（2）如图二，当动点D在等边三角形ABC边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCE和等边三角形DCF，连接AE，BF，探究AE，BF与AB有何数量关系？并证明你探究的结论．
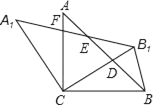
（3）如图三，当动点D在等边三角形ABC边BA的延长线上运动时，其他作法与图2相同，若AE＝8，BF＝2，请直接写出AB＝ ．
【答案】（1）见解析。（2）见解析。（3）6.
【解析】
（1）由等边三角形的性质可得AC＝BC，DC＝CE，∠ACB＝∠DCE＝60°，可得∠ACE＝∠BCD，根据“SAS”可证△BCD≌△ACE，即AE＝BE；
（2）由等边三角形的性质可得AC＝BC，DC＝CF，∠ACB＝∠DCF＝60°，可得∠FCB＝∠DCA，根据“SAS”可证△ACD≌△BCF，即BF＝AD，即可得AB＝AE＝BF；
（3）根据等边三角形的性质和全等三角形的判定和性质可得AE＝BD，BF＝AD，即可求AB的长．
（1）AE＝BD
理由如下：∵△ABC和△DCE是等边三角形
∴AC＝BC，DC＝CE，∠ACB＝∠DCE＝60°，
∴∠ACE＝∠BCD，且AC＝BC，DC＝CE
∴△BCD≌△ACE（SAS）
∴AE＝BD
（2）AB＝AE+BF，
理由如下：∵△ABC和△DCF是等边三角形，
∴AC＝BC，CF＝CD，∠FCD＝∠BCA＝60°，
∴∠FCB＝∠DCA，且AC＝BC，CF＝CD，
∴△ACD≌△BCF（SAS）
∴BF＝AD，
由（1）可知，BD＝AE，
∵AB＝BD+AD，
∴AB＝AE+BF
（3）∵△ABC和△DCE是等边三角形，
∴AC＝BC，DC＝CE，∠ACB＝∠DCE＝60°，
∴∠BCD＝∠ACE，且AC＝BC，DC＝CE，
∴△BCD≌△ACE（SAS）
∴AE＝BD＝8，
∵△ABC和△DCF是等边三角形，
∴AC＝BC，CF＝CD，∠FCD＝∠BCA＝60°，
∴∠FCB＝∠DCA，且AC＝BC，CF＝CD，
∴△ACD≌△BCF（SAS）
∴BF＝AD＝2，
∵AB＝BD﹣AD
∴AB＝8﹣2＝6
故答案为：6
