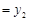题目内容
已知点E 、F
、F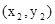 在抛物线
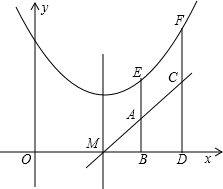
在抛物线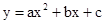 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
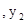 的数量关系式为:S=
的数量关系式为:S=
 、F
、F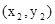 在抛物线
在抛物线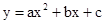 的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
的对称轴的同侧 (点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积,.则S与
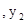 的数量关系式为:S=
的数量关系式为:S= 
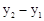 .
.试题分析:首先根据题意可求得:y1,y2的值,A与C的坐标,即可用x1与x2表示出AB,CD,BD的值,易得四边形ABCD是直角梯形,即可得S=
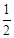 (AB+CD)•BD,然后代入其取值,整理变形,即可求得S与y1、y2的数量关系式:
(AB+CD)•BD,然后代入其取值,整理变形,即可求得S与y1、y2的数量关系式:根据题意得:
 ,
,∵点A、C在直线y=2ax+b上,∴点A的坐标为:(x1,2ax1+b),点C的坐标为:(x2,2ax2+b).
∴AB=2ax1+b,CD=2ax2+b,BD=
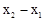 .
.∵EB⊥BD,CD⊥BD,∴AB∥CD. ∴四边形ABCD是直角梯形.
∴
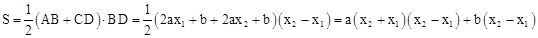
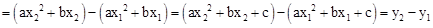
∴S与y1、y2的数量关系式为:S=
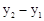 .
.
练习册系列答案
相关题目
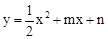 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.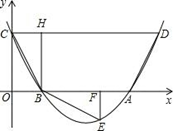
 2,4) 和点B (1,0)都在抛物线
2,4) 和点B (1,0)都在抛物线 上.
上.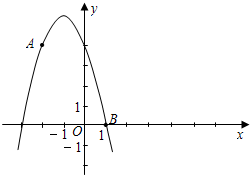
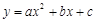 (
( >0)的对称轴为直线
>0)的对称轴为直线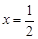 ,且经过点(-3,
,且经过点(-3, ),(4,
),(4, ),试比较
),试比较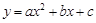 (
(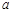 <0)过
<0)过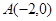 、
、 、
、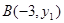 、
、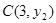 四点,则
四点,则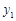 与
与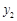 的大小关系是( )
的大小关系是( )