题目内容
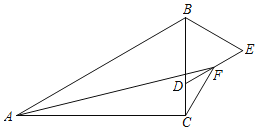
【题目】如图所示,已知△ABC和△DCE均是等边三角形,点B. C. E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是( )个

A.1B.2C.3D.4
【答案】D
【解析】
首先根据等边三角形的性质,得到BC=AC,CD=CE,∠ACB=∠BCD=60°,然后由SAS判定△BCD≌△ACE,根据全等三角形的对应边相等即可证得①正确;又由全等三角形的对应角相等,得到∠CBD=∠CAE,根据ASA,证得△BCF≌△ACG,即可得到②正确,同理证得CF=CG,得到△CFG是等边三角形,易得③正确.
首先根据等边三角形的性质,得到BC=AC,CD=CE∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
∴△BCD≌△ACE(SAS),
∴AE=BD,(①正确)
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,AC=BC,
∴△BCF≌△ACG(ASA),
∴AG=BF,(②正确)
同理:△DFC≌△EGC(ASA),
∴CF=CG,
∴△CFG是等边三角形,
∴∠CFG=∠FCB=60°,
∴FG∥BE,(③正确)
过C作CM⊥AE于M,CN⊥BD于N,
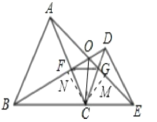
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵CD=CE,∠CND=∠CMA=90°,
∴△CDN≌△CEM,
∴CM=CN,
∵CM⊥AE,CN⊥BD,
∴△Rt△OCN≌Rt△OCM(HL)
∴∠BOC=∠EOC,
∴④正确;
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目