题目内容
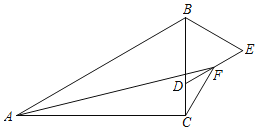
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是_____.
【答案】2![]() .
.
【解析】
以BC为边作等边三角形BCG,连接FG,AG,作GH⊥AC交AC的延长线于H,根据等边三角形的性质得到DC=EG,根据全等三角形的性质得到FC=FG,于是得到在点D的运动过程中,AF+FC=AF+FG,而AF+FG≥AG,当F点移动到AG上时,即A,F,G三点共线时,AF+FC的最小值=AG,根据勾股定理即可得到结论.
以BC为边作等边三角形BCG,连接FG,AG,
作GH⊥AC交AC的延长线于H,
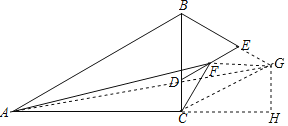
∵△BDE和△BCG是等边三角形,
∴DC=EG,
∴∠FDC=∠FEG=120°,
∵DF=EF,
∴△DFC≌△EFG(SAS),
∴FC=FG,
∴在点D的运动过程中,AF+FC=AF+FG,而AF+FG≥AG,
∴当F点移动到AG上时,即A,F,G三点共线时,AF+FC的最小值=AG,
∵BC=CG=![]() AB=2,AC=2
AB=2,AC=2![]() ,
,
在Rt△CGH中,∠GCH=30°,CG=2,
∴GH=1,CH=![]() ,
,
∴AG=![]() =
=![]() =2
=2![]() ,
,
∴AF+CF的最小值是2![]() .
.

练习册系列答案
相关题目