题目内容
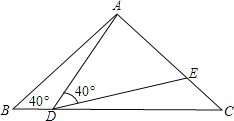
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
【答案】(1)25°;小.(2)当DC等于2时,△ABD≌△DCE;(3)当∠ADB=110°或80°时,△ADE是等腰三角形.
【解析】
试题分析:(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据点D的运动方向可判定∠BDA的变化情况.
(2)假设△ABD≌△DCE,利用全等三角形的对应边相等得出AB=DC=2,即可求得答案.
(3)假设△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD,根据三角形的内角和定理求出∠ADB.
解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2)当△ABD≌△DCE时.
DC=AB,
∵AB=2,
∴DC=2,
∴当DC等于2时,△ABD≌△DCE;
(3)∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.

【题目】2012年7月1日起,重庆实施阶梯电价,市民家庭每月用电量使用情况不同,按照用电量区间价格缴纳用电费用.其收费标准如下表:阶梯电价分三个档次.设某用户每月用电量为x度,应交电费为y元.
档次 | 用电量 | 每度电价格 |
第一档 | 不超过200度的部分 | 0.52元 |
第二档 | 超过200度不超过400度的部分 | 0.57元 |
第三档 | 超过400度的部分 | 0.82元 |
(1)直接写出y与x的关系式;
(2)小明家6、7月份共用电800度,应交电费471元,已知7月份的用电量比6月份的用电量大,求小明家6、7月份各用电多少度?






