Question

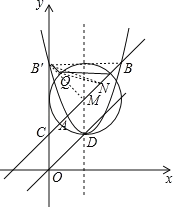
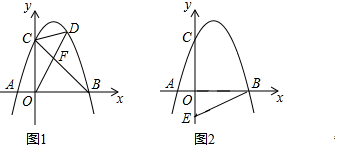
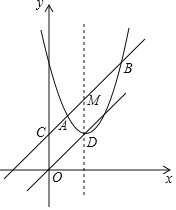
【题目】如图，直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点（A在B的左侧），与y轴交于点C，抛物线的顶点为D，抛物线的对称轴与直线AB交于点M．

（1）当四边形CODM是菱形时，求点D的坐标；

（2）若点P为直线OD上一动点，求△APB的面积；

（3）作点B关于直线MD的对称点B'，以点M为圆心，MD为半径作⊙M，点Q是⊙M上一动点，求QB'+QB的最小值．

Answer 1

【答案】（1）D（，）；（2）3；（3）．

【解析】

（1）求出D（m，m），C（0，2），根据菱形的性质可得OD=OC=2=m，求出m＝，则D点坐标可求出；

（2）联立直线与抛物线求出交点A、B的坐标，然后求出AB的长，再根据AB∥OD求出两平行线间的距离，最后根据三角形的面积公式列式计算即可得解；

（3）根据A、B的坐标求出AM、BM的长，再根据点M的坐标，从而得到⊙M的半径为2，取MB的中点N，连接QB、QN、QB′，然后利用两边对应成比例夹角相等两三角形相似求出△MNQ和△MQB相似，再根据相似三角形对应边成比例求出，然后根据三角形任意两边之和大于第三边判断出Q、N、B′三点共线时QB’+最小，然后根据勾股定理列式计算即可得解．

解：（1）∵抛物线y=x2﹣2mx+m2+m=（x-m）2+m，直线y=x+2，

∴D（m，m），C（0，2），

∴OD=m，

∵四边形CODM为菱形，

∴OD=OC=2=m，

∴m=，

∴D（）；

（2）∵y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点，

∴联立，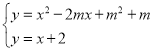

解得：，，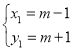

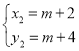∵点A在点B的左侧，

∴A（m﹣1，m+1），B（m+2，m+4），

∴AB==3，

∵D（m，m），

∴直线OD的解析式为y=x，

∵直线AB的解析式为y=x+2，

∴AB∥OD，

如图，作CE⊥OD于E，则∠COE＝45°，

∴直线AB、OD之间的距离CE=×2=，

∴S△APB=ABCE=×3×=3；

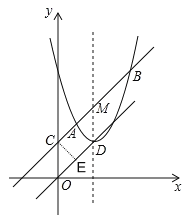
（3）∵抛物线对称轴为x=m，当x=m时，y=x+2=m+2，

∴M（m，m+2），

又∵A（m﹣1，m+1），B（m+2，m+4），

∴AM=1×=，BM=2×=2，

∵D（m，m），

∴以MD为半径的圆的半径为 （m+2）﹣m=2，

取MB的中点N，连接QB、QN、QB'，

∴MN=BN=，

∵，∠QMN=∠BMQ，

∴△MNQ∽△MQB，

∴，

∴，

∴当Q、N、B'三点共线时QB'+QB最小，

∵直线AB的解析式为y=x+2，

∴直线AB与对称轴夹角为45°，

∵点B、B'关于对称轴对称，

∴∠BMB'=90°，

由勾股定理得：QB'+QB的最小值为B'N==，即QB'+QB的最小值是．