题目内容
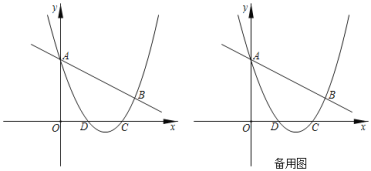
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)点P的坐标为(1,﹣6)或(1,﹣![]() ).
).
【解析】
(1)由点A的坐标及抛物线的对称轴可得出AE=2,利用二次函数的性质可得出BE=2,结合tan∠BDE=![]() ,可得出DE的长度,进而可得出点D的坐标,抛物线的表达式可设为y=a(x﹣1)2﹣4,根据点A的坐标,利用待定系数法可求出a的值,进而可得出抛物线的表达式;
,可得出DE的长度,进而可得出点D的坐标,抛物线的表达式可设为y=a(x﹣1)2﹣4,根据点A的坐标,利用待定系数法可求出a的值,进而可得出抛物线的表达式;
(2)取点F(5,0),连接DF,过点C作CM⊥直线DE,垂足为点M,过点B作BN⊥直线DF,垂足为点N,则△DEF,△BNF为等腰直角三角形,根据等腰直角三角形的性质可求出BN,DN的长度,进而可得出tan∠BDN=![]() ,利用二次函数图象上点的坐标特征可得出点C的坐标,结合点D的坐标可得出△CDM为等腰直角三角形,分点P在点D的下方和点P在点D的上方两种情况考虑:①当点P在点D下方时,由∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°可得出∠CPM=∠BDN,进而可得出tan∠CPM=
,利用二次函数图象上点的坐标特征可得出点C的坐标,结合点D的坐标可得出△CDM为等腰直角三角形,分点P在点D的下方和点P在点D的上方两种情况考虑:①当点P在点D下方时,由∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°可得出∠CPM=∠BDN,进而可得出tan∠CPM=![]() =
=![]() ,代入CM=1可求出MP,进而可求出点P的坐标;②当点P在点D上方时,由∠PCD+∠PCM=45°,∠BDE+∠BDN=45°可得出∠PCM=∠BDN,进而可得出tan∠PCM=
,代入CM=1可求出MP,进而可求出点P的坐标;②当点P在点D上方时,由∠PCD+∠PCM=45°,∠BDE+∠BDN=45°可得出∠PCM=∠BDN,进而可得出tan∠PCM=![]() =
=![]() ,代入CM=1可求出MP,进而可求出点P的坐标.综上,此题得解.
,代入CM=1可求出MP,进而可求出点P的坐标.综上,此题得解.
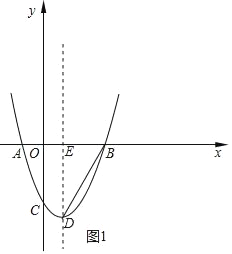
(1)依照题意,画出图形,如图1所示.
∵点A的坐标为(﹣1,0),抛物线的对称轴为直线x=1,
∴点E的坐标为(1,0),
∴BE=AE=2.
∵tan∠BDE=![]() =
=![]() ,
,
∴DE=2BE=4,
∴点D的坐标为(1,﹣4).
∴抛物线的表达式可设为y=a(x﹣1)2﹣4.
将(﹣1,0)代入y=a(x﹣1)2+4,得:4a﹣4=0,
解得:a=1,
∴抛物线的表达式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3.
(2)取点F(5,0),连接DF,过点C作CM⊥直线DE,垂足为点M,过点B作BN⊥直线DF,垂足为点N,如图2所示.
∵点D的坐标为(1,﹣4),
∴EF=DE=4,
∴△DEF为等腰直角三角形,
∴∠EDF=∠EFD=45°,DF=4![]() .
.
∵BN⊥DF,
∴△BNF为等腰直角三角形,
∴NB=NF=![]() BF=
BF=![]() ,
,
∴DN=DF﹣NF=3![]() ,
,
∴tan∠BDN=![]() =
=![]() .
.
当x=0时,y=x2﹣2x﹣3=﹣3,
∴点C的坐标为(0,﹣3).
∵点D的坐标为(1,﹣4),CM⊥DE,
∴CM=DM=1,
∴△CDM为等腰直角三角形,
∴∠DCM=∠CDM=45°.
①当点P在点D下方时,∵∠CDM=∠DCP+∠CPM=45°,∠BDE+∠BDN=45°,
∴∠CPM=∠BDN,
∴tan∠CPM=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MP=3,
∴EP=EM+MP=6,
∴点P的坐标为(1,﹣6);
②当点P在点D上方时,∵∠PCD+∠PCM=45°,∠BDE+∠BDN=45°,
∴∠PCM=∠BDN,
∴tan∠PCM=![]() =
=![]() ,
,
∴MP=![]() ,
,
∴EP=EM+MP=![]() ,
,
∴点P的坐标为(1,﹣![]() ).
).
综上所述,点P的坐标为(1,﹣6)或(1,﹣![]() ).
).

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣![]() <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
A. 4个 B. 3个 C. 2个 D. 1个