题目内容
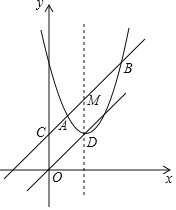
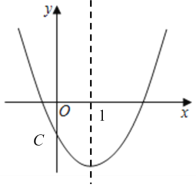
【题目】如图是二次函数y＝ax2+bx+c图象的一部分，且过点（﹣3，0），（1，0），下列说法错误的是（ ）
A.2a﹣b＝0
B.4a﹣2b+c＜0
C.（﹣4，y1），（2，y2）是抛物线上两点，则y1＞y2
D.y＜0时，﹣3＜x＜1
【答案】C
【解析】
根据抛物线的对称轴为x＝
＝﹣1判断A；二次函数的图象判断B；根据抛物线的对称轴为x＝﹣1判断C；根据二次函数的图象判断D．
解：A、∵过点（﹣3，0），（1，0），
∴对称轴为直线x＝
＝＝﹣1，
∴b＝2a，即2a﹣b＝0，故正确；
B、∴当x＝﹣2时，y＜0，
∴4a﹣2b+c＜0，故正确；
C、∵抛物线的对称轴为x＝﹣1，
∴x＝﹣4与x＝2时的y值相等，
∴y1＝y2，故错误；
D、抛物线开口向上且过点（﹣3，0），（1，0），
∴y＜0时，﹣3＜x＜1，故正确；
故选：C．
练习册系列答案
相关题目
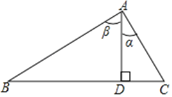
【题目】如图，在△ABC中，∠C=60°，BC=3厘米，AC=4厘米，点P从点B出发，沿B→C→A以每秒1厘米的速度匀速运动到点A．设点P的运动时间为x秒，B、P两点间的距离为y厘米．
小新根据学习函数的经验，对函数
随自变量
的变化而变化的规律进行了探究．
下面是小新的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x（s） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y（cm） | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是（保留一位小数）．
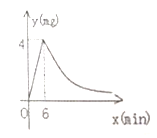
（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC中画出点P所在的位置．