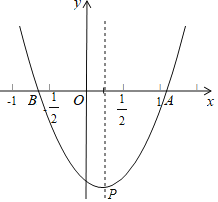题目内容
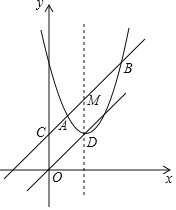
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式;
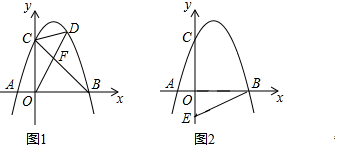
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点D(1,4)或(2,3);(3)当点P在x轴上方时,点P(![]() ,
,![]() );当点P在x轴下方时,点(﹣
);当点P在x轴下方时,点(﹣![]() ,﹣
,﹣![]() )
)
【解析】
(1)c=3,点B(3,0),将点B的坐标代入抛物线表达式:y=ax2+2x+3,解得a=﹣1即可得出答案;
(2)由S△COF:S△CDF=3:2得OF:FD=3:2,由DH∥CO得CO:DM=3:2,求得DM=2,而DM=![]() =2,即可求解;
=2,即可求解;
(3)分点P在x轴上方、点P在x轴下方两种情况,分别求解即可.
(1) ∵OB=OC=3,
∴点C的坐标为C(0,3),c=3,点B的坐标为B(3,0),
将点B的坐标代入抛物线表达式:y=ax2+2x+3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)如图,过点D作DH⊥x轴于点H,交BC于点M,
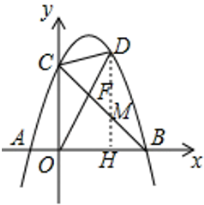
∵S△COF:S△CDF=3:2,
∴OF:FD=3:2,
∵DH∥CO,
∴CO:DM= OF:FD=3:2,
∴DM=![]() CO=2,
CO=2,
设直线BC的表达式为:![]() ,
,
将C(0,3),B(3,0)代入得![]() ,
,
解得:![]() ,
,
∴直线BC的表达式为:y=﹣x+3,
设点D的坐标为(x,﹣x2+2x+3),则点M(x,﹣x+3),
∴DM=![]() =2,
=2,
解得:x=1或2,
故点D的坐标为:(1,4)或(2,3);
(3)①当点P在x轴上方时,
取OG=OE,连接BG,过点B作直线PB交抛物线于点P,交y轴于点M,使∠GBM=∠GBO,
则∠OBP=2∠OBE,过点G作GH⊥BM,如图,

∵点E的坐标为(0,![]() ),
),
∴OE=![]() ,
,
∵∠GBM=∠GBO,GH⊥BM,GO⊥OB,
∴GH= GO=OE=![]() ,BH=BO=3,
,BH=BO=3,
设MH=x,则MG= ,
,
在△OBM中,OB2+OM2=MB2,即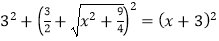 ,
,
解得:x=2,
故MG=![]() =
=![]() ,则OM=MG+ GO=
,则OM=MG+ GO=![]() +
+![]() ,
,
点M的坐标为(0,4),
设直线BM的表达式为:![]() ,
,
将点B(3,0)、M(0,4)代入得:![]() ,
,
解得: ,
,
∴直线BM的表达式为:y=![]() x+4,
x+4,
解方程组
解得:x=3(舍去)或![]() ,
,
将x=![]() 代入 y=
代入 y=![]() x+4得y=
x+4得y=![]() ,
,
故点P的坐标为(![]() ,
,![]() );
);
②当点P在x轴下方时,如图,过点E作EN⊥BP,直线PB交y轴于点M,
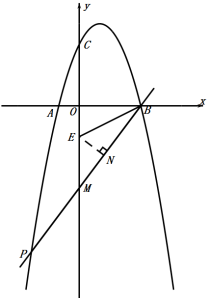
∵∠OBP=2∠OBE,
∴BE是∠OBP的平分线,
∴EN= OE=![]() ,BN=OB=3,
,BN=OB=3,
设MN=x,则ME= ,
,
在![]() △OBM中,OB2+OM2=MB2,即
△OBM中,OB2+OM2=MB2,即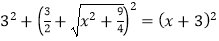 ,
,
解得:![]() ,
,
∴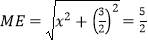 ,则OM=ME+ EO=
,则OM=ME+ EO=![]() +
+![]() ,
,
点M的坐标为(0,-4),
设直线BM的表达式为:![]() ,
,
将点B(3,0)、M(0,-4)代入得:![]() ,
,
解得: ,
,
∴直线BM的表达式为:![]() ,
,
解方程组
解得:x=3(舍去)或![]() ,
,
将x=![]() 代入
代入![]() 得
得![]() ,
,
故点P的坐标为(![]() ,
,![]() );
);
综上,点P的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .

 阅读快车系列答案
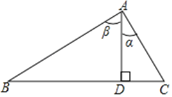
阅读快车系列答案【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.

小新根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(cm) | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是(保留一位小数).
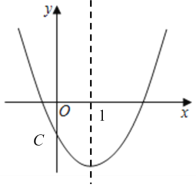
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.