Question

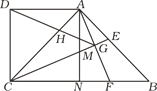
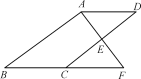
【题目】如图，E是□ABCD的边CD的中点，延长AE交BC的延长线于点F．

(1)求证：AE=EF；

(2)若∠BAF=90°，BC=15，EF=9，求CD的长．

Answer 1

【答案】（1）详见解析；（2）CD=24

【解析】

（1）要证明AE=EF，只要证明△AED≌△FEC即可，根据平行四边形的性质和全等三角形的判定即可解答本题；
（2）根据（1）中的结论和勾股定理、平行四边形的性质可以求得CD的长．

（1）证明：∵四边形ABCD是平行四边形，点E时CD的中点，
∴AD∥BF，ED=EC，
∴∠D=∠ECF，
在△AED和△FEC中，
∠D=∠ECF，ED=EC，∠AED=∠FEC，
∴△AED≌△FEC（ASA），
∴AE=EF；
（2）由（1）知△AED≌△FEC，
∴AD=FC，
∵四边形ABCD是平行四边形，∠BAF=90°，BC=15，EF=9，AE=AF，
∴AD=BC=15，AB=CD，AF=2EF=18，
∴BF=2BC=30，
∴在Rt△ABF中，由勾股定理得：AB=，
∴CD=AB=24．