题目内容
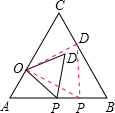
如图，在等边△ABC中，AC=3，点O在AC上，且AO=1．点P是AB上一点，连接OP，以线段OP为一边作正△OPD，且O、P、D三点依次呈逆时针方向，当点D恰好落在边BC上时，则AP的长是（ ）
| A．1 | B．1.5 | C．2 | D．3 |
∵∠C=∠A=∠DOP=60°，OD=OP，
∴∠CDO+∠COD=120°，∠COD+∠AOP=120°，
∴∠CDO=∠AOP．
在△ODC和△POA中，
，
∴△ODC≌△POA（AAS）．
∴AP=OC．
∴AP=OC=AC-AO=2．
故选：C．
∴∠CDO+∠COD=120°，∠COD+∠AOP=120°，
∴∠CDO=∠AOP．
在△ODC和△POA中，
|
∴△ODC≌△POA（AAS）．
∴AP=OC．
∴AP=OC=AC-AO=2．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
