题目内容
如图，在△ABC中，AB=AC，D是三角形外一点，且∠ABD=60°，BD+DC=AB．求证：∠ACD=60°．
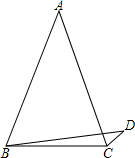
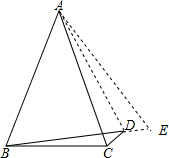
证明：延长BD至E，使CD=DE，连接AE，AD，
∵BD+CD=AB，BE=BD+DE，
∴BE=AB，
∵∠ABD=60°，
∴△ABE是等边三角形，
∴AE=AB=AC，∠E=60°，
在△ACD和△ADE中，
，
∴△ACD≌△ADE（SSS），
∴∠ACD=∠E=60°．
∵BD+CD=AB，BE=BD+DE，
∴BE=AB，
∵∠ABD=60°，
∴△ABE是等边三角形，
∴AE=AB=AC，∠E=60°，
在△ACD和△ADE中，
|
∴△ACD≌△ADE（SSS），
∴∠ACD=∠E=60°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
