题目内容
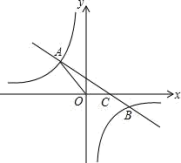
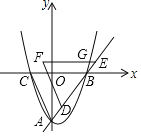
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,抛物线
与x轴交于点B,与y轴交于点A,抛物线![]() 经过A,B两点,与x轴的另一交点为C.
经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)将△ABC以每秒1个单位的速度沿射线AB方向平移,平移后的三角形记为△DEF,平移时间为t秒,0≤t≤5,平移过程中EF与抛物线交于点G.
①当FG:GE=3:2时,求t的值;
②△DEF与△AOB重叠部分面积为S,直接写出S与t的函数关系式.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)①t=
x﹣4;(2)①t=![]() ;②S=
;②S=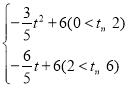
【解析】
(1)点A、B的坐标分别为:(0,﹣4)、(3,0),c=﹣4,抛物线的表达式为:y=![]() x2+bx﹣4,将点B的坐标代入上即可求解;
x2+bx﹣4,将点B的坐标代入上即可求解;
(2)①设点E(x,![]() t),FG:GE=3:2,则3EG=2FG,即3(3+
t),FG:GE=3:2,则3EG=2FG,即3(3+![]() ﹣x)=2(x+2﹣
﹣x)=2(x+2﹣![]() ),即可求解;
),即可求解;
②当0<t≤2时,S=S△BRF﹣S△OHR;②当2<t≤5时,S=![]() OB×|yD|,即可求解.
OB×|yD|,即可求解.
解:(1)直线![]() 与x轴交于点B,与y轴交于点A,
与x轴交于点B,与y轴交于点A,
令y=0,则x=3,令x=0,则y=﹣4,
故点A、B的坐标分别为:(0,﹣4)、(3,0),
c=﹣4,抛物线的表达式为:y=![]() x2+bx﹣4,
x2+bx﹣4,
将点B的坐标代入上式并解得:b=﹣![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)设△ABC沿AB移动了t个单位,则向右移动了![]() t个单位、向上移动了
t个单位、向上移动了![]() t个单位,
t个单位,
则点E、F、D的坐标分别为:(3+![]() t,
t,![]() t),(﹣2+
t),(﹣2+![]() t,
t,![]() t)、(
t)、(![]() t,﹣4+
t,﹣4+![]() t);
t);
①设点E(x,![]() t),
t),
FG:GE=3:2,则3EG=2FG,
即3(3+![]() ﹣x)=2(x+2﹣
﹣x)=2(x+2﹣![]() ),
),
化简得:x=1+![]() ,
,
将点E(1+![]() ,
,![]() )的坐标代入抛物线表达式并整理得:
)的坐标代入抛物线表达式并整理得:
3t2+3t﹣50=0,
解得:t=![]() (不合题意的值已舍去);
(不合题意的值已舍去);
②当0<t≤2时,
如下图所示,设直线FD与x、y轴分别交于点R、H,
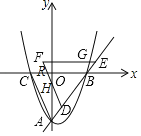
由点A、C的坐标可得,直线AC的表达式为:y=﹣2x﹣4,
则设直线FD的表达式为:y=﹣2x+b,
将点D的坐标代入上式并解得:b=2t﹣4,
故直线FD的表达式为:y=﹣2x+2t﹣4,
则点R、H的坐标分别为:(t﹣2,0)、(2t﹣4);
S=S△BRF﹣S△OHR
=![]() BR×|yD|﹣
BR×|yD|﹣![]() ×OR×OH
×OR×OH
=![]() (3﹣t+2)(﹣
(3﹣t+2)(﹣![]() t+4)﹣
t+4)﹣![]() (2﹣t)(4﹣2t)
(2﹣t)(4﹣2t)
=﹣![]() t2+6;
t2+6;
②当2<t≤5时,
S=![]() OB×|yD|=
OB×|yD|=![]() ×3×(4﹣
×3×(4﹣![]() t)=﹣
t)=﹣![]() t+6;
t+6;
综上,S=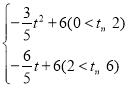 .
.