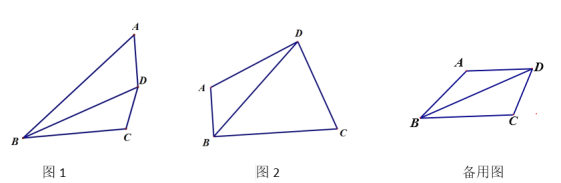
��Ŀ����
����Ŀ����֪����x�Ķ��κ���y=ax2-(2a+2)x+b(a��0)��x=0��x=6ʱ����ֵ���.
(1)��a��ֵ;
(2)���ö��κ�����ͼ����ֱ��y=-2x��һ������Ϊ(2,m),�����Ľ���ʽ;
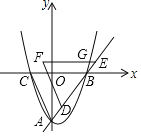
(3)��(2)��������,ֱ��y=-2x-4��x��,y��ֱ���A,B,���߶�AB����ƽ��n(n>0)����λ,ͬʱ���ö��κ�����2��x��7�IJ�������ƽ��n����λ��õ���ͼ���ΪG,����ͼ��ֱ�ӻش�,��ͼ��G��ƽ�ƺ���߶��й�����ʱ,n��ȡֵ��Χ.
���𰸡�(1) x=3,a=![]() (2) y=
(2) y=![]() x2-3x(3)n=1��2��n��4,
x2-3x(3)n=1��2��n��4,
��������
(1)�ɵö��κ���x=3�������a��ֵ��
��2�����������Ϊ(2,-4)�����루1������ʽ�ɵö��κ����Ľ���ʽ��
(3)�������A��B�����꼰ֱ��y=-2x-4����ƽ��n(n>0)����λ�ı���ʽ�����κ�����2��x��7�IJ�������ƽ��n����λ��õ���ͼ���ΪG���ɵ�G�ĺ�������ʽ�����������ķ����н⣬�ɵ�n��ȡֵ��Χ.
(1)�߶��κ�����x=0��x=6ʱ����ֵ���,
��ö��κ����ĶԳ���Ϊx=3
��x=![]() ,
,
�Ⲣ�����:a=![]() .
.
(2)��ֱ��y=-2x����(2,m),
��m=-2��2=-4,
������,��(2,-4)����������,
����(1)a=![]() ,������Ϊy=
,������Ϊy=![]() x2-3x+b,
x2-3x+b,
�ɵ�:2-6+b=-4,
���b=0,
�������ߵĽ���ʽΪy=![]() x2-3x.
x2-3x.
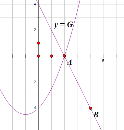
(3)����ͼ��
��n=1ʱ��һ�κ���Ϊ![]() (-1��x��1),GΪ
(-1��x��1),GΪ![]() (1��x��6)���й������㣨1��-4������n=1��������;
(1��x��6)���й������㣨1��-4������n=1��������;
��
��n=2ʱ, ![]() (0��x��2), GΪ
(0��x��2), GΪ![]() (0��x��5), �й������㣨2��-4������n=2��������
(0��x��5), �й������㣨2��-4������n=2��������
��
��n=4ʱ, ![]() (2��x��4), GΪ
(2��x��4), GΪ![]() (-2��x��3),��ʱ�й����㣨2��0��
(-2��x��3),��ʱ�й����㣨2��0��
�ʣ�n=1��2��n��4,

 ��������ϵ�д�
��������ϵ�д�