题目内容
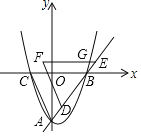
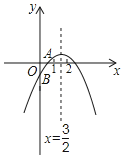
【题目】如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（
，0），与y轴的交点B在（0，0）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝
．则下列结论：① x＞3时，y＜0；② 4a+b＜0；③﹣
＜a＜0；④ 4ac+b2＜4a．其中正确的是（ ）
A.②③④B.①②③C.①③④D.①②④
【答案】B
【解析】
由已知可得a＜0，对称轴为x＝
，抛物线与x轴的两个交点为（
，0），（
，0），可得b＝﹣3a，所以① 当x＞3时，y＜0；② 4a+b＝4a-3a＝a＜0；③ 又由c＝
a，﹣1＜c＜0，可得﹣
＜a＜0；④ 因为将b＝﹣3a，c＝a代入4ac+b2﹣4a即可判断正误．
解：由图象可知，抛物线开口向下，则a＜0，
∵对称轴为直线x＝，
∴x＝0与x＝3所对应的函数值相同，
∵当x＝0时,y＜0，
∴x＝3时,y＜0，
∴x＞3时，y＜0，
∴①正确；
∵x＝＝﹣
，
∴b＝﹣3a，
∴4a+b＝4a﹣3a＝a＜0，
∴②正确；
∵抛物线经过点A（，0），
∴
a+b+c＝0，
∴c＝a，
∵B在（0，0）和（0，﹣1）之间，
∴﹣1＜c＜0，
∴﹣1＜a＜0，
∴﹣＜a＜0，
∴③正确；
4ac+b2﹣4a＝4a×a+(﹣3a)2﹣4a＝5a2+9a2-4a＝14a2﹣4a＝2a(7a﹣2)，
∵a＜0，
∴2a（7a﹣2）＞0，
∴4ac+b2﹣4a＞0，
∴④不正确；
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
