题目内容
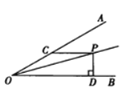
【题目】如图,∠AOB=30°,OP平分∠AOB,PC∥OB交OA于点C,PD⊥OB于点D,如果PC=6,那么PD的长是_________________.
【答案】3
【解析】
根据角平分线的性质,角平分线上的点到两角的距离相等,因而过P作PE⊥OA于点E,则PD=PE,因为PC∥OB,根据三角形的外角的性质得到:∠ECP=∠COP+∠OPC=30°,在直角△ECP中求得PE的长即可得出PD的长.
解:过P作PE⊥OA于点E,则PD=PE,
∵PC∥OB,
∴∠OPC=∠POD,
又∵OP平分∠AOB,∠AOB=30°,
∴∠OPC=∠COP=15°,
∴∠ECP=∠COP+∠OPC=30°,
在直角△ECP中,
PE=![]() PC=3,
PC=3,
则PD=PE=3.
故答案为:3.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
【题目】某服装店用10000元购进A,B两种新式服装,按标价售出后可获得毛利润5400元(毛利润=售价﹣进价),这两种服装的进价、标价如表所示:
类型、价格 | A型 | B型 |
进价(元/件) | 80 | 100 |
标价(元/件) | 120 | 160 |
(1)这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,要使这批服装全部售出后毛利润不低于2000元,则B种服装至多按标价的几折出售?