Question

【题目】如图，∠AOB=90°，OM平分∠AOB，直角三角板的直角顶点P在射线OM上移动，两直角边分别与OA、CB相交于点C、D．

（1）问PC与PD相等吗？试说明理由．

（2）若OP=2，求四边形PCOD的面积．

Answer 1

【答案】(1)见解析;(2)2.

【解析】

（1）过P分别作PE⊥OB于E，PF⊥OA于F，由角平分线的性质易得PE=PF，然后由同角的余角相等证明∠1=∠2，即可由ASA证明△CFP≌△DEP，从而得证；

（2）只要证明四边形PCOD的面积=正方形OEPF的面积即可.

（1）结论：PC=PD．

理由：如图，

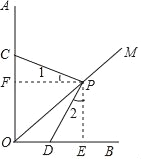
过P分别作PE⊥OB于E，PF⊥OA于F，

∴∠CFP=∠DEP=90°，

∵OM是∠AOB的平分线，

∴PE=PF，

∵∠1+∠FPD=90°，∠AOB=90°，

∴∠FPE=90°，

∴∠2+∠FPD=90°，

∴∠1=∠2，

在△CFP和△DEP中，，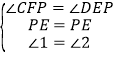

∴△CFP≌△DEP（ASA），

∴PC=PD；

（2）∵四边形PCOD的面积=正方形OEPF的面积，

∴四边形PCOD的面积=×2×2=2．