题目内容
【题目】如图①，在地面上有两根等长的立柱AB，CD，它们之间悬挂了一根抛物线形状的绳子，按照图中的直角坐标系，这条绳子可以用y= 
x2﹣ 
x+3表示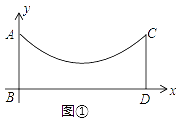 
（1）求这条绳子最低点离地面的距离；
（2）现由于实际需要，要在两根立柱之间再加一根立柱EF对绳子进行支撑（如图②），已知立柱EF到AB距离为3m，两旁的绳子也是抛物线形状，且立柱EF左侧绳子的最低点到EF的距离为1m，到地面的距离为1.8m，求立柱EF的长．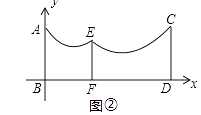
【答案】
（1）
解：∵y= 
x2﹣ 
x+3= （x﹣4）2+ 
，
∴抛物线的顶点坐标为（4， ），
则这条绳子最低点离地面的距离为 m
（2）
解：对于y= x2﹣ x+3，当x=0时，y=3，即点A坐标为（0，3），
由题意，立柱EF左侧绳子所在抛物线的顶点为（2，1.8），
∴可设其解析式为y=a（x﹣2）2+1.8，
把x=0、y=3代入，得：3=a（0﹣2）2+1.8，
解得：a= 
，
∴y= （x﹣2）2+1.8，
当x=3时，y= （3﹣2）2+1.8=2.1，
∴立柱EF的长为2.1m
【解析】（1）将抛物线解析式配方成顶点式即可得出答案；（2）由原抛物线解析式求得点A坐标，根据EF左侧抛物线顶点坐标设出解析式，将A坐标代入求得其解析式，再求出x=3时y的值即可．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
