题目内容
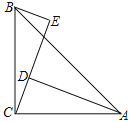
【题目】如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.

(1)若∠ECD=60°,求∠AFC的度数;
(2)若∠ECD=∠BAF,试判断∠ABD与∠BDC之间的数量关系,并说明理由.
【答案】(1)∠AFC=120°(2)∠ABD=∠BDC
【解析】(1)根据已知条件得到∠BMF=∠BNC,由平行线的判定定理得到AF∥CE,根据平行线的性质得到∠AFC+∠ECD=180°,即可得到结论;
(2)由∠AFC+∠ECD=180°,由于∠ECD=∠BAF,等量代换得到∠BAF+∠AFC=180°,推出AB∥CD,根据平行线的性质即可得到结论.
(1)∵∠AMD=∠BNC,
∵∠AMD=∠BMF,
∴∠BMF=∠BNC,
∴AF∥CE,
∴∠AFC+∠ECD=180°,
∵∠ECD=60°,
∴∠AFC=120°;
(2)∵∠AFC+∠ECD=180°,
∵∠ECD=∠BAF,
∴∠BAF+∠AFC=180°,
∴AB∥CD,
∴∠ABD=∠BDC.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)