题目内容
【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰Rt△,则点D的坐标为 .
【答案】(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】解:①如图1中,当∠ADP=90°,D在AB下方,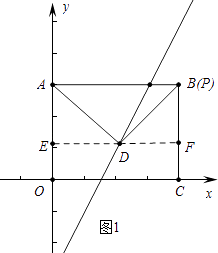
设点D坐标(a,2a﹣6),过点D作EF∥OC交OA于E,交BC于F,
则OE=2a﹣6,AE=AO﹣OE=12﹣2a,
在△ADE和△DPF中,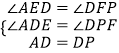
∴△ADE≌△DPF,
∴AE=DF=12﹣2a,
∵EF=OC=8,
∴a+12﹣2a=8,
∴a=4.
此时点D坐标(4,2).②如图2中,当∠ADP=90°,D在AB上方,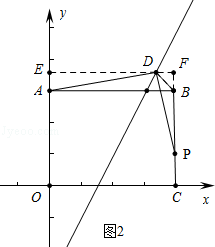
设点D坐标(a,2a﹣6),过点D作EF∥OC交OA于E,交CB的延长线于F,
则OE=2a﹣6,AE=OE﹣OA=2a﹣12,
由△ADE≌△DPF,得到DF=AE=2a﹣12,
∵EF=8,
∴a+2a﹣12=8,
∴a= ![]() ,
,
此时点D坐标( ![]() ,
, ![]() ).③如图3中,当∠APD=90°时,
).③如图3中,当∠APD=90°时,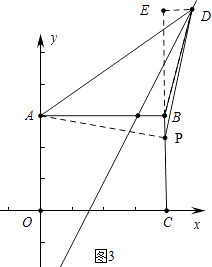
设点D坐标(a,2a﹣6),作DE⊥CB的延长线于E.同理可知△ABP≌△EPD,
∴AB=EP=8,PB=DE=a﹣8,
∴EB=2a﹣6﹣6=8﹣(a﹣8),
∴a= ![]() ,
,
此时点D坐标( ![]() ,
, ![]() ).
).
当∠DAP=90°时,此时P在BC的延长线上,
∴点D坐标为(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
所以答案是(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).

练习册系列答案
相关题目