题目内容
【题目】在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2 个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢,赢的一方得电影票.
(1)游戏规则1:两人各摸1个球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
(2)游戏规则2; 两人同时各摸1个球,若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏小明赢得电影票的概率为 .
【答案】(1)此游戏不公平(2)![]()
【解析】试题分析:(1)游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
(2)本题可通过列表法或画树状图法来求,解题时要注意:(1)摸出小球后记下颜色放回与不放回的区别;(2)把红球标记为红1和红2,保证每次摸球的可能性相等.
试题解析:
(1)此游戏不公平.
理由如下:列树状图如下,
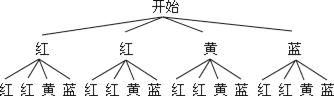
列表如下,
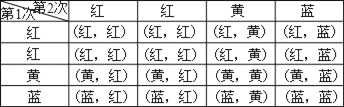
由上述树状图或表格知:所有可能出现的结果共有16种.
P(小明赢)=![]() ,P(小亮赢)=
,P(小亮赢)=![]() .
.
∴此游戏对双方不公平,小亮赢的可能性大;
(2)列表如下:
红1 | 红2 | 黄 | 蓝 | |
红1 | 红1红1 | 红1红2 | 红1黄 | 红1蓝 |
红2 | 红2红1 | 红2红2 | 红2黄 | 红2蓝 |
黄 | 黄 红1 | 黄 红2 | 黄黄 | 黄蓝 |
蓝 | 蓝 红1 | 蓝 红2 | 蓝黄 | 蓝蓝 |
由表格可知,共有16种等可能的结果,其中两球颜色相同的情况有6种,故小明赢得门票的概率为![]() .
.
故答案为: ![]() .
.

【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.





