��Ŀ����
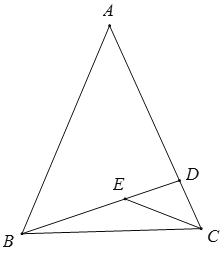
����Ŀ���ڡ�ABC�У�AB=BC����ABC=90�㣮��ABΪб��������ֱ��������ADB����P��ֱ��DB��һ�����㣬����AP����PE��AP��BC���ڵ�ֱ���ڵ�E��
��1����ͼ1����P��BD���ӳ����ϣ�PE��EC��AD=1��ֱ��д��PE�ij���
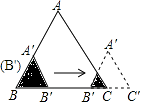
��2����P���߶�BD�ϣ�����B��D�غϣ��������⣬��ͼ2��ȫ����֤��PA=PE��
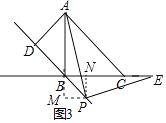
��3����P��DB���ӳ����ϣ������⣬��ͼ3��ȫ�����ж�PA=PE�Ƿ���Ȼ������
���𰸡�
��1��
�⣺��AD=DB=1����ADB=90�㣬
���ABP=45�㣬AB= ![]() =
= ![]() ��
��
��PE��AP��AB��BC��
��PA��EC��
��PA��AB��
���ı���ABEP�Ǿ��Σ�
�ߡ�ABP=45�㣬
��PA=AB��
���ı���ABEP�������Σ�
��PE=AB= ![]()
��2��
�⣺�ߡ�ABC�͡�ADB�ǵ���ֱ�������Σ�
���ADB=90�㣬��DAB=��DBA=45�㣬
���PBN=45��
��PE��AP����DAP=��BPE=90�㩁��DPA��
�ߡ�PAM=45�㩁��DAP����PEN=45�㩁��BPE��
���PAM=��PEN��
��P��PM��AB�ڵ�M����P��PN��BC�ڵ�N��

��PM=PN����BPN=45�㣬
�ڡ�APM�͡�EPN�У�  ��
��
���APM�ա�EPN��
��PA=PE��
��3��
�⣺�ߡ�ABC�͡�ADB�ǵ���ֱ�������Σ�
���ABD=45�㣬
���PBN=45�㣬��ABC=90�㣬
��P��PM��AB�ڵ�M����P��PN��BC�ڵ�N��
���ı���BMPN�Ǿ��Σ�
�ߡ�NBP=45�㣬
���ı���BMPN�������Σ�
��PM=PN��
��AB��BC��
���BAN=��APN��
��AP��PE��
���APN=��E��
���BAP=��E��
�ڡ�AMP���ENP�У�  ��
��
���AMP�ա�ENP��
��AP=PE��
����������1�����ݵ���ֱ�������ε����ʵõ���ABP=45�㣬���ݹ��ɶ����õ�AB= ![]() =
= ![]() ���Ƴ��ı���ABEP�Ǿ��Σ��õ��ı���ABEP�������Σ����ǵõ����ۣ���2�����ݵ���ֱ�������ε����ʵõ���ADB=90�㣬��DAB=��DBA=45�㣬��á�PBN=45���P��PM��AB�ڵ�M����P��PN��BC�ڵ�N�����ǵõ�PM=PN����BPN=45�����ȫ�������ε����ʼ��ɵõ����ۣ���3�����ݵ���ֱ�������ε����ʵõ���ABD=45�㣬�õ���PBN=45�㣬��ABC=90�㣬��P��PM��AB�ڵ�M����P��PN��BC�ڵ�N���õ��ı���BMPN�Ǿ��Σ��Ƴ��ı���BMPN�������Σ��õ�PM=PN������ȫ�������ε����ʼ��ɵõ����ۣ�
���Ƴ��ı���ABEP�Ǿ��Σ��õ��ı���ABEP�������Σ����ǵõ����ۣ���2�����ݵ���ֱ�������ε����ʵõ���ADB=90�㣬��DAB=��DBA=45�㣬��á�PBN=45���P��PM��AB�ڵ�M����P��PN��BC�ڵ�N�����ǵõ�PM=PN����BPN=45�����ȫ�������ε����ʼ��ɵõ����ۣ���3�����ݵ���ֱ�������ε����ʵõ���ABD=45�㣬�õ���PBN=45�㣬��ABC=90�㣬��P��PM��AB�ڵ�M����P��PN��BC�ڵ�N���õ��ı���BMPN�Ǿ��Σ��Ƴ��ı���BMPN�������Σ��õ�PM=PN������ȫ�������ε����ʼ��ɵõ����ۣ�
�����㾫�������յ���ֱ�������κ������ε��ж������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻���ж�һ���ı����Ǿ��Σ����ж�����һ���ڱ���ȣ����ж�һ���ı��������Σ����ж�����һ������ֱ�ǣ�

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
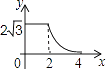
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�����Ŀ��������һ�����⣺̽������y= ![]() ��
�� ![]() x��ͼ�������ʣ� С������ѧϰ�����ľ��飬�Ժ���y=
x��ͼ�������ʣ� С������ѧϰ�����ľ��飬�Ժ���y= ![]() ��
�� ![]() x��ͼ�������ʽ�����̽����
x��ͼ�������ʽ�����̽����
������С����̽�����̣��벹�������������������⣺
��1������y= ![]() ��
�� ![]() x���Ա���x��ȡֵ��Χ����
x���Ա���x��ȡֵ��Χ����
��2���±���y��x�ļ����Ӧֵ����m��ֵ��
x | �� | ��4 | ��3 | ��2 | �� | ��1 | �� | | 1 | 2 | 3 | 4 | �� |
y | �� | | | | | | | | | �� | �� | m | �� |
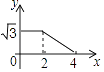
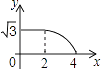
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ�� 
��4����һ��̽�����֣��ú���ͼ���ڵڶ������ڵ���͵�������ǣ���2�� ![]() ������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��
������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ� ��
��5�����ݺ���ͼ����㷽�� ![]() ��
�� ![]() x=2�ĸ�Ϊ �� ����ȷ��0.1��
x=2�ĸ�Ϊ �� ����ȷ��0.1��