题目内容
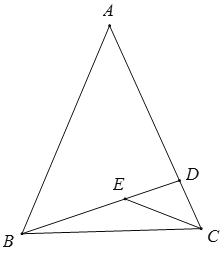
【题目】如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.
(1)试求∠ABD的度数;
(2)求证:∠BEC>∠A.
【答案】(1)45°;(2)证明见解析.
【解析】
(1)依据三角形的内角和是180°,可求∠A=45°,∠B=60°,∠C=75°.又BD⊥AC,所以∠ABD=45°.
(2)依据三角形的外角大于与它不相邻的任一内角,可证∠BEC>∠BDC>∠A,即∠BEC>∠A.
(1)∵∠A+∠ABC+∠ACB=180°,∠A:∠ABC:∠ACB=3:4:5,
∴∠A=45°,∠B=60°,∠C=75°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD=90°-∠A=45°;
(2)∵∠BEC是△CDE的外角,
∴∠BEC>∠BDC,
∵∠BDC是△ABD的外角,
∴∠BDC>∠A,
∴∠BEC>∠A.

练习册系列答案
相关题目