Question

如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的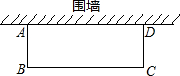总长度是6m．（可利用的围墙长度超过6m）．
（1）若矩形的面积为4m²，求边AB的长度；
（2）当边AB的长度为多少时矩形的面积最大？最大面积为多少？

Answer 1

（1）设AB长为x米，则BC长为（6-2x）米．
依题意，得x（6-2x）=4．
整理，得x2-3x+2=0．
解方程，得x₁=1，x₂=2．
所以当x=1时，6-2x=4；
当x=2时，6-2x=2（不符合题意，舍去）．
答：AB的长为1米；

（2）设矩形花圃ABCD的面积为S．
S=x（6-2x）=-2x²+6x=-2（x-

3

2

）²+

9

2

，
∴当x=

3

2

时，S_最大=

9

2

，
∴当边AB的长度为

3

2

m时，矩形的面积最大为

9

2

m²