Question

【题目】已知圆O的直径AB=12，点C是圆上一点，且∠ABC=30°，点P是弦BC上一动点，过点P作PD⊥OP交圆O于点D．

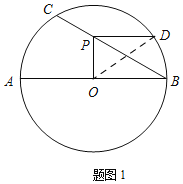
（1）如图1，当PD∥AB 时，求PD的长；

（2）如图2，当BP平分∠OPD时，求PC的长．

Answer 1

【答案】（1）PD=;(2)PC=3

【解析】

（1）先判断出∠POB=90°，进而求出OP＝OBtan30°＝2最后用勾股定理即可得出结论；

（2）先求出OH＝OB＝3，BH＝OBcos30°＝3，进而求出CH＝BH＝3，即可得出结论．

解：如图1，连接OD .

∵直径AB=12

∴OB=OD=6

∵PD⊥OP

∴∠DPO=90°

∵PD∥AB

∴∠DPO+∠POB=180°

∴∠POB=90°

又∵∠ABC=30°，OB=6

∴，

∵在Rt△POD 中，PO2+PD2=OD2

∴,

∴;

（2）如图2，过点O 作OH⊥BC，垂足为H

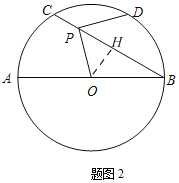
∵OH⊥BC

∴∠OHB=∠OHP=90°

∵∠ABC=30°，OB=6

∴，，

∵在⊙O 中，OH⊥BC

∴.

∵BP 平分∠OPD

∴∠BPO=∠DPO=45°，

∴PH=OHcot45°=3

∴PC=CH-PH=．