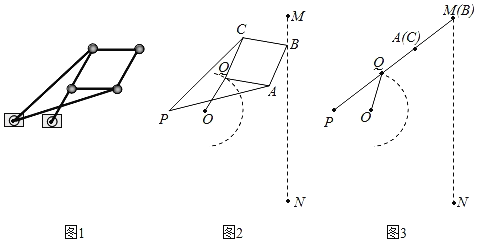
题目内容
【题目】在平面直角坐标系中,O为原点,点![]() ,点
,点 .
.
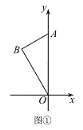
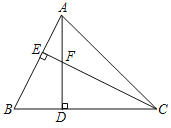
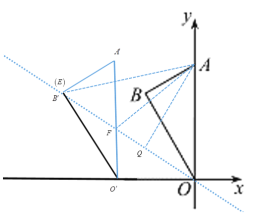
(1)如图①,求![]() 的长;
的长;
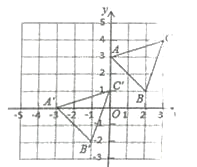
(2)将![]() 沿x轴向左平移,得到
沿x轴向左平移,得到![]() ,点O,A,B的对应点分别为
,点O,A,B的对应点分别为![]() ,
,![]() ,
,![]() .
.
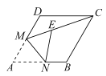
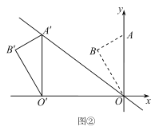
①如图②,当点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标;
的坐标;
②设![]() ,其中
,其中![]() ,
,![]() 的边与直线
的边与直线![]() 交于E,F两点,求
交于E,F两点,求![]() 的最大值(直接写出结果即可).
的最大值(直接写出结果即可).
【答案】(1)3;(2)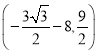 ;(3)
;(3)![]()
【解析】
(1)过点B作![]() 轴于点H,利用勾股定理可得答案;
轴于点H,利用勾股定理可得答案;
(2)①利用![]() 落在
落在![]() 上,求解
上,求解![]() 的坐标,求解
的坐标,求解![]() 的长,利用平移的性质得到
的长,利用平移的性质得到![]() 的坐标;②当
的坐标;②当![]() 与
与![]() 重合时,三角形
重合时,三角形![]() 面积最大,过
面积最大,过![]() 作
作![]() 于
于![]() ,由
,由![]() 利用一次函数的性质与平移的性质,勾股定理求解
利用一次函数的性质与平移的性质,勾股定理求解![]() 即可得到答案.
即可得到答案.
解:(1)如图,过点B作![]() 轴于点H.
轴于点H.
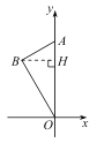
∵点![]() ,点
,点 ,
,
∴![]() ,
,![]() ,
,![]() .
.
![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
∴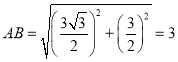
(2)①如图,设点![]() .
.

由平移可得![]() ,
,![]() ,
,![]() .
.
∵点![]() 落在直线
落在直线![]() 上,
上,
∴![]() .解得
.解得![]() .
.
∴![]() .
.
∴点![]() 的坐标为
的坐标为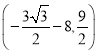 .
.
②如图,当![]() 落在
落在![]() 上时,
上时,
则![]()
![]()
![]()
![]()
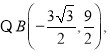
![]()
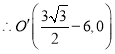
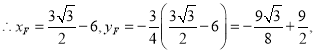
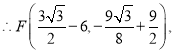
过![]() 作
作![]() 于
于![]() ,由
,由![]()
当![]() 与
与![]() 重合时,三角形
重合时,三角形![]() 面积最大,
面积最大,
![]()
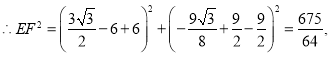
![]()
![]() 为
为![]()
![]()
![]()
![]()
![]()
设![]() 则
则![]()
![]()
![]()
![]()
即三角形![]() 的面积最大值是
的面积最大值是![]()

练习册系列答案
相关题目
【题目】2019年10月1日是新中国成立70周年.某学校国庆节后,为了调查学生对这场阅兵仪式的关注情况,在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试,批改试卷后,学校政教处随机抽取了部分学生的考卷进行成绩统计,发现成绩最低是51分,最高是100分,根据统计结果,绘制了如下尚不完整的统计图表.
调查结果频数分布表
分数段/分 | 频数 | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
| 0.25 |
| 35 |
|
| 12 | 0.12 |
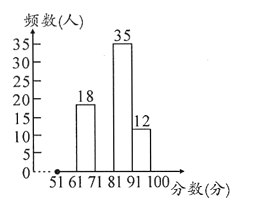
请根据以上信息,解答下列问题:
(1)![]() ;
;
(2)若把上面频数分布表中的信息画在扇形统计图内,则![]() 所在扇形圆心角的度数是 ;
所在扇形圆心角的度数是 ;
(3)请将频数分布直方图补充完整;
(4)若该校有1200名学生,请估计该校分数![]() 在
在![]() 范围的学生有多少名.
范围的学生有多少名.