Question

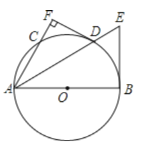
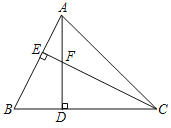
【题目】如图，在△ABC中，tan∠B＝2，∠ACB＝45°，AD⊥BC于点D，CE⊥AB于点E，AD、CE交于点F，若AC＝5，则线段EF的长为_____．

Answer 1

【答案】

【解析】

根据题意先证明△ADC为等腰直角三角形，再由正弦函数求得AD与CD的长，由同角的余角相等及对顶角相等证得∠DFC=∠AFE=∠B，然后根据tan∠DFC=2求得DF的长，从而可得AF的长；根据tan∠AFE=tan∠B=2，设AE=2x，EF=x，由勾股定理表示出AF，利用EF=AFcos∠AFE求得EF的长即可．

解：∵在△ABC中，∠ACB＝45°，AD⊥BC于点D，

∴△ADC为等腰直角三角形，

∴AD＝CD，

∵AC＝5，

∴AD＝CD＝ACsin45°＝5×＝5，

∵AD⊥BC于点D，CE⊥AB于点E，

∴∠B+∠BAD＝∠AFE+∠BAD＝90°，

∴∠DFC＝∠AFE＝∠B，

∵tan∠B＝2，

∴tan∠DFC＝2，

∴＝2，

∴DF＝＝，

∴AF＝AD﹣DF＝5﹣＝，

∵tan∠AFE＝tan∠B＝2，

∴设AE＝2x，EF＝x，由勾股定理得AF＝x＝，

∴EF＝x＝，

故答案为：．