Question

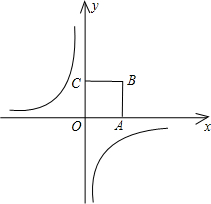如图，正方形OABC的边长为2，顶点A在x轴的正半轴上，将这个正方形向下平移1个单位，得到O′A′B′C′，A′落在双曲线y=

k

x

的图象上．
（1）试求双曲线y=

k

x

的函数关系式；
（2）若将正方形OABC向左平移后，BC与双曲线相交于C₁，C₁是否在直线A′C′上？

Answer 1

分析：（1）首先根据正方形的性质与平移规律可以得到A的坐标，然后利用待定系数法确定反比例函数的解析式；
（2）根据平移规律确定A'、C'两点的坐标，然后利用待定系数法确定直线A'C'的解析式，再根据已知条件可以确定C₁的坐标，代入A'C'的解析式就可以判断C₁是否在直线A'C'上．

解答：解：（1）∵正方形OABC边长为2，∴OA=2，
正方形向下平移1个单位，平移后点A′的坐标为（2，-1），（1分）
∴-1=

k

2

，k=-2；（2分）
∴双曲线的关系式是y=-

2

x

；（3分）

（2）设平移后直线A′C′方程为y=kx+b，（4分）
由点A′（2，-1）、C′（0，1）在直线A′C′上得

2k+b=-1 b=1

，（5分）
解得

k=-1 b=1

，所以y=-x+1，
解方程组

y=- 2 x y=2

得C′（-1，2），（8分）
∵2=-（-1）+1，∴C′在直线A′C′上．

点评：此题主要考查了用待定系数法确定一次函数，反比例函数的解析式，也利用坐标平移的知识．