题目内容
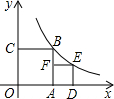如图，正方形OABC、ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B、E在函数y=| 4 | x |
（1）求正方形OABC的面积；
（2）求E点坐标．
分析：（1）因为B点在函数图象上，所以正方形的面积为k的值．
（2）因为E点也在反比例函数图象上，且四边形ADEF是正方形，可利用OD和DE为边构成的长方形的面积求解．
（2）因为E点也在反比例函数图象上，且四边形ADEF是正方形，可利用OD和DE为边构成的长方形的面积求解．
解答：解：（1）正方形OABC面积为OA•AB，
设B的坐标为（x，y），
∵xy=4，
∴正方形OABC面积为4；
（2）设ED=y，则OD=2+y．
由y（2+y）=4，
y2+2y-4=0，
解得y=-1±
（舍去y=-1-
），
∴E（1+
，-1+
）．
设B的坐标为（x，y），
∵xy=4，
∴正方形OABC面积为4；
（2）设ED=y，则OD=2+y．
由y（2+y）=4，
y2+2y-4=0，
解得y=-1±
| 5 |
| 5 |
∴E（1+
| 5 |
| 5 |
点评：本题考查反比例函数的综合运用，关键是知道函数图象上的点和坐标轴构成的四边形的面积和系数的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
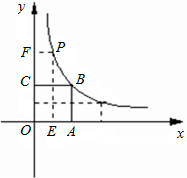的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S．（提示：考虑点P在点B的左侧或右侧两种情况）
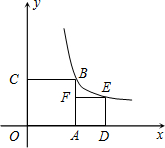如图，正方形OABC和正方形ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数y=
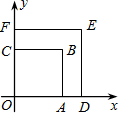如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为
象上，点P（m，n）是函数