题目内容
【题目】如图1,已知抛物线![]() 过点
过点![]() .
.
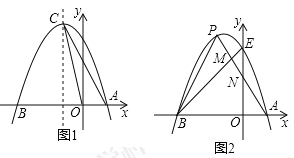
(1)求抛物线的解析式及其顶点C的坐标;
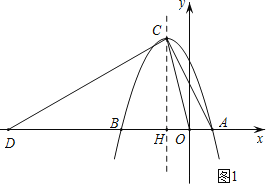
(2)设点D是x轴上一点,当![]() 时,求点D的坐标;
时,求点D的坐标;
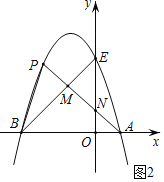
(3)如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,顶点C的坐标为-(-1,4);(2)
,顶点C的坐标为-(-1,4);(2)![]() ;(3)
;(3)![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)利用待定系数法,将A,B的坐标代入![]() 即可求得二次函数的解析式;
即可求得二次函数的解析式;
(2)设抛物线对称轴与x轴交于点H,在![]() 中,可求得
中,可求得![]() ,推出
,推出![]() ,可证
,可证![]() ,利用相似三角形的性质可求出AD的长度,进一步可求出点D的坐标,由对称性可直接求出另一种情况;
,利用相似三角形的性质可求出AD的长度,进一步可求出点D的坐标,由对称性可直接求出另一种情况;
(3)设![]() 代入
代入![]() ,求出直线PA的解析式,求出点N的坐标,由
,求出直线PA的解析式,求出点N的坐标,由![]() ,可推出
,可推出![]() ,再用含a的代数式表示出来,最终可用函数的思想来求出其最大值.
,再用含a的代数式表示出来,最终可用函数的思想来求出其最大值.
解:(1)由题意把点![]() 代入
代入![]() ,
,
得,![]() ,
,
解得![]() ,
,
![]()
![]()
∴此抛物线解析式为:![]() ,顶点C的坐标为
,顶点C的坐标为![]()
(2)∵抛物线顶点![]() ,
,
∴抛物线对称轴为直线![]() ,
,
设抛物线对称轴与x轴交于点H,
则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
∴当![]() 时,
时,
![]()
如图1,当点D在对称轴左侧时,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
当点D在对称轴右侧时,点D关于直线![]() 的对称点D'的坐标为
的对称点D'的坐标为![]() ,
,
∴点D的坐标为![]() 或
或![]() ;
;
(3)设![]() ,
,
将![]() 代入
代入![]() ,
,
得,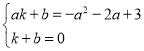 ,
,
解得,![]() ,
,
![]()
当![]() 时,
时,![]() ,
,
![]()
如图2,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
由二次函数的性质知,当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
![]() 和
和![]() 的面积分别为m、n,
的面积分别为m、n,
![]() 的最大值为
的最大值为![]() .
.

 阅读快车系列答案
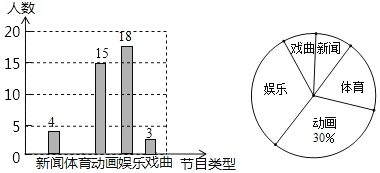
阅读快车系列答案【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.