Question

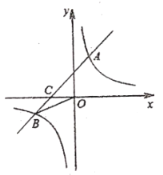
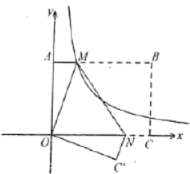
【题目】如图，在平面直角坐标系中，、分别为轴、轴正半轴上的点，以、为边，在一象限内作矩形，且．将矩形翻折，使点与原点重合，折痕为，点的对应点落在第四象限，过点的反比例函数，其图象恰好过的中点，则点的坐标为________．

Answer 1

【答案】（，）．

【解析】

连接BO与MN交于点Q，过点Q作QG⊥x轴，垂足为G，可通过三角形全等证得BO与MN的交点就是MN的中点Q，由相似三角形的性质可得S△OGN= S△OCB，根据反比例函数比例系数的几何意义可求出k，从而求出S△OAM，进而可以得到AB=4AM，即BM=3AM．由轴对称的性质可得OM=BM，从而得到OM=3AM，也就有AO=2AM，根据△OAM的面积可以求出AM，OA的值．易证四边形OAEH为矩形，从而得到MH=OA，就可求出MH的值，问题得解．

解：连接BO与MN交于点Q，过点Q作QG⊥x轴，垂足为G，如图所示，

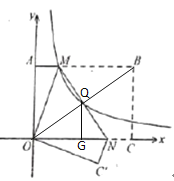
∵矩形OABC沿MN翻折，点B与点O重合，

∴BQ=OQ，BM=MO．

∵四边形OABC是矩形，

∴AB∥CO，∠BCO=∠OAB=90°．

∴∠MBQ=∠NOQ．

在△BMQ和△ONQ中， ．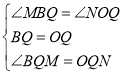

∴△BMQ≌△ONQ（ASA）．

∴MQ=NQ．

∴点Q是MN的中点．

∵∠QGO=∠BCO=90°，

∴QG∥BC．

∴△OGQ∽△OCB．

∴．

∵S矩形OABC= ，

∴S△OCB=S△OAB=．

∴．

∵点Q在反比例函数y=上，

∴，解得：．

∴S△OAM= ．

∵S△OAB= ，

∴AB=4AM．

∴BM=3AM．

由轴对称的性质可得：OM=BM．

∴OM=3AM．OA=

∴S△OAM=AOAM=×2AM×AM=．

解得：AM=．

∴OA=2×= ．

∴M点坐标为（，）．

故答案为：（，）．