题目内容
【题目】已知∠MON=90°，有一根长为10的木棒AB的两个端点A、B分别在射线OM,ON上滑动，∠OAB的角平分线AD交OB于点D.
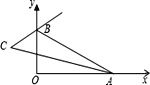
（1）如图（1），若OA=6，则OB= ，OD= ；
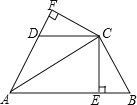
（2）如图（2），过点B作BE⊥AD,交AD的延长线于点E,连接OE,在AB滑动的过程中，线段OE,BE有何数量关系，并说明理由；
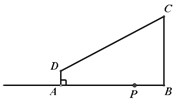
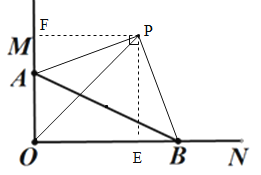
（3）若点P是∠MON内部一点，在（1）的条件下，当△ABP是以AB为斜边的等腰直角三角形时，OP2= ；
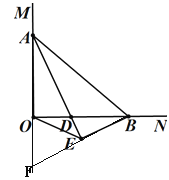
（4）在AB滑动的过程中，△AOB面积的最大值为 .
·图（1） 图（2） 备用图
【答案】（1）8；3；（2）相等；(3)98;(4)25.
【解析】试题分析：（1）由勾股定理得到OB的长．由角平分线性质得到OD的长；
（2）延长BE交AO的延长线于F点．证明△BAE≌△FAE，得到BE=EF．
再由直角三角形斜边上的直线等于斜边的一半即可得到结论．
（3）过P作PE⊥OB于E，PF⊥OM于F．则△PFA≌△PEB，FOEP是正方形，设OE=x，则PE=x，EB=8-x，MA=x-6，由8-x=x-6，解方程得到x的值，在Rt△OEP中，由勾股定理即可得到结论；
（4）设OA=x，OB=y，面积为S，则S= 
， 
，由
，得到
，故
，从而有S= 
≤25，即可得到结论．
试题解析：解：（1）∵AB=10，AO=6，∴OB= 8．∵AD平分∠OAB，∴OA：AB=OD：DB，∴6：10=OD：（8-OD），解得： OD=3；
（2）相等 ．理由如下：
延长BE交AO的延长线于F点．∵AE是∠BAO的角平分线，∴∠BAE=∠FAE．
∵BE⊥AD，∴∠AEF=∠AEB=90°．∵AE=AE，∴△BAE≌△FAE，∴BE=EF．
在Rt△BOF中， ∠BOF=90°，∴OE=BE．
（3）过P作PE⊥OB于E，PF⊥OM于F．∵AP=BP，∠APB=90°，∴AP=BP=
AB=
.∵∠PFO=∠PEO=∠BOA=90°，∴∠EPF=90°，∴∠FPA=∠EPB．在△PFA和△PEB中，∵∠FPA=∠EPB，∠PFA=∠PEB，PA=PB，∴△PFA≌△PEB，∴PF=PE，FA=EB，∴FOEP是正方形，∴PF=OE=PE=FO，设OE=x，则PE=x，EB=8-x，MA=x-6，∴8-x=x-6，解得：x=7，在Rt△OEP中， 
=
=98；
（4）解：设OA=x，OB=y，面积为S，则S= 
， 
，∵
，∴
，∴ 
，∴xy≤50，∴S= 
≤25．∴△AOB面积的最大值为25．
