题目内容
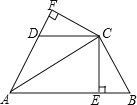
【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
【答案】(1)证明见解析;(2)4;(3)2.5.
【解析】试题分析:(1)根据HL证明Rt△BCE与Rt△DCF全等,再利用全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可;
(3)利用三角形的面积公式解答即可.
试题解析:解:(1)相等,∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,∴CE=CF,在Rt△BCE与Rt△DCF中,∵CE=CF,BC=CD,∴Rt△BCE≌Rt△DCF(HL),∴BE=DF;
(2)∵Rt△BCE≌Rt△DCF,∴DF=EB,CE=CF,CE⊥AB于E,CF⊥AD于F,在Rt△ACE与Rt△ACF中,∵CE=CF,AC=AC,∴Rt△ACERt△ACF(HL),∴AF=AE,∵DF=1,AD=3,∴AB=AF+BE=AD+DF+BE=5;
(3)∵Rt△BCE≌Rt△DCF,∵△ABC的面积是23,△ADC面积是18,∴△BEC的面积=![]() ×(23-18)=2.5.
×(23-18)=2.5.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目