题目内容
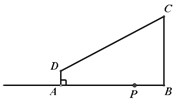
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2㎝,BC=6㎝,AB=7㎝,点P是从点B出发在射线BA上的一个动点,运动的速度是1㎝/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
A.5个
B.4个
C.3个
D.2个
【答案】A
【解析】
试题分析:因为AD∥BC,∠ABC=90°,所以∠A=∠ABC=90°,设点P运动t秒钟时,△PAD与△PBC是相似三角形,当点P在线段BA上时,因为AD=2㎝,BC=6㎝,AB=7㎝,所以PB=t,PA=7-t,(1)当△PAD∽△PBC时,有![]() ,所以
,所以![]() ,解得t=
,解得t=![]() ;(2)当△PAD∽△CBP时,有
;(2)当△PAD∽△CBP时,有![]() ,所以
,所以![]() ,解得t=3,t=4;当点P在线段BA的延长线上时,PB=t,PA=t-7,同理:当△PAD∽△PBC时,解得t=
,解得t=3,t=4;当点P在线段BA的延长线上时,PB=t,PA=t-7,同理:当△PAD∽△PBC时,解得t=![]() ;当△PAD∽△CBP时,解得t=
;当△PAD∽△CBP时,解得t=![]() ,因为t>0,所以t=
,因为t>0,所以t=![]() ,综上所述,t=
,综上所述,t=![]() 或t=3或t=4或t=
或t=3或t=4或t=![]() 或t=
或t=![]() ,所以满足条件的点P共有5个,故选:A.
,所以满足条件的点P共有5个,故选:A.

练习册系列答案
相关题目