题目内容
 (2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.
(2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.(1)求过C、B、A三点的二次函数的解析式;
(2)若(1)中抛物线的顶点是M,判定△MDC的形状,并说明理由.
分析:(1)△OCD是由△OBA旋转所得,因此OB=OC、OA=OD,所以由OA、OB的长,即可得出A、B、C、D四点的坐标,利用待定系数法即可求出过C、B、A三点的二次函数的解析式.
(2)由(1)的二次函数解析式不难求出顶点M的坐标,在已知M、C、D三点坐标的情况下,由坐标系两点间的距离公式可求出MD、CD、MC三边的长,再由三边长来判断△MCD的形状.
(2)由(1)的二次函数解析式不难求出顶点M的坐标,在已知M、C、D三点坐标的情况下,由坐标系两点间的距离公式可求出MD、CD、MC三边的长,再由三边长来判断△MCD的形状.
解答:解:(1)由题意知,C、B、A三点的坐标分别为:C(-3,0)、B(0,3)、A(1,0);
设二次函数的解析式为y=a(x-1)(x+3),依题意,有:
a(0-1)(0+3)=3,解得:a=-1
故过C、B、A三点的二次函数的解析式为y=-x2-2x+3.
(2)△MDC是等腰直角三角形,理由如下:
由(1)知,抛物线的解析式:y=-x2-2x+3=-(x+1)2+4,则M(-1,4);
易知:C(-3,0)、D(0,1),则:
MC2=(-1+3)2+(4-0)2=20,MD2=(-1-0)2+(4-1)2=10,CD2=(-3-0)2+(0-1)2=10
则MC2=MD2+CD2,且MD=CD,
因此△MDC为等腰直角三角形.
设二次函数的解析式为y=a(x-1)(x+3),依题意,有:
a(0-1)(0+3)=3,解得:a=-1
故过C、B、A三点的二次函数的解析式为y=-x2-2x+3.
(2)△MDC是等腰直角三角形,理由如下:
由(1)知,抛物线的解析式:y=-x2-2x+3=-(x+1)2+4,则M(-1,4);
易知:C(-3,0)、D(0,1),则:
MC2=(-1+3)2+(4-0)2=20,MD2=(-1-0)2+(4-1)2=10,CD2=(-3-0)2+(0-1)2=10
则MC2=MD2+CD2,且MD=CD,
因此△MDC为等腰直角三角形.
点评:此题考查的内容较为简单,主要涉及旋转图形的性质、利用待定系数法确定二次函数的解析式以及等腰直角三角形的判定;(2)的解法较多,也可过M作y轴的垂线,通过构建全等三角形来解.

练习册系列答案
相关题目
 (2004•泰安)如图,在△ABC中,AB=AC,点E、D、F在边BC上,且∠BAD=∠CAD.BE=CF,则图中全等的三角形共有( )
(2004•泰安)如图,在△ABC中,AB=AC,点E、D、F在边BC上,且∠BAD=∠CAD.BE=CF,则图中全等的三角形共有( )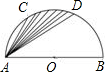 (2004•泰安)如图,点C、D是以AB为直径的半圆的三等分点,弧CD的长为
(2004•泰安)如图,点C、D是以AB为直径的半圆的三等分点,弧CD的长为 (2004•泰安)如图,AB是⊙O的弦,P是AB上一点,AB=10cm,PA:PB=2:3,OP=5cm,则⊙O的半径等于
(2004•泰安)如图,AB是⊙O的弦,P是AB上一点,AB=10cm,PA:PB=2:3,OP=5cm,则⊙O的半径等于 (2004•泰安)如图,在△ABC中,AB=3,BC=
(2004•泰安)如图,在△ABC中,AB=3,BC=