Question

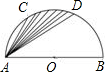（2004•泰安）如图，点C、D是以AB为直径的半圆的三等分点，弧CD的长为

1

3

π，则图中阴影部分的面积为（　　）

• A．

  1

  6

  π
• B．

  3

  16

  π
• C．

  1

  24

  π
• D．

  1

  12

  π+

  1

  4

  3

Answer 1

分析：连接CO、DO和CD，利用等底等高的三角形面积相等可知S_阴影=S_扇形COD，利用扇形的面积公式计算即可．

解答：解：连接CO、DO和CD，如下图所示，

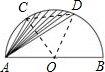
∵C，D是以AB为直径的半圆上的三等分点，弧CD的长为

1

3

π，
∴∠COD=60°，圆的半周长=πr=3×

1

3

π=π，
∴r=1，
∵△ACD的面积等于△OCD的面积，
∴S_阴影=S_扇形OCD=

60π×12

360

=

π

6

．
故选A．

点评：本题考查扇形面积的计算，解题关键是根据“点C、D是以AB为直径的半圆的三等分点，弧CD的长为

1

3

π”求出圆的半径，继而利用扇形的面积公式求出S_阴影=S_扇形COD．