题目内容
 (2004•泰安)如图,在△ABC中,AB=3,BC=2
(2004•泰安)如图,在△ABC中,AB=3,BC=2| 2 |
| 2 |
(1)求S与x之间的函数关系式;
(2)是否存在点M,使△AMN的面积等于4?若存在,求出CM的长;若不存在,请说明理由.
分析:(1)连接CN.MN平行AC,根据等底等高的三角形面积相等可得到S△CMN=S△AMN,利用相似三角形的性质可得到BN的长,作NH垂直BM于H,解直角三角形BNH可求出NH的长,继而求出S与x之间的函数关系式;
(2)不存在点M,使△AMN的面积等于4,设三角形AMN的面积为4,由(1)的函数关系可得一元二次方程无解,所以假设不成立.
(2)不存在点M,使△AMN的面积等于4,设三角形AMN的面积为4,由(1)的函数关系可得一元二次方程无解,所以假设不成立.
解答:解:(1)连接CN.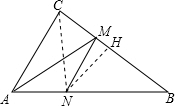
∵MN∥AC,
∴S△CMN=S△AMN,
∵CM=x,则BM=2
-x,
∴△BMN∽BCA,
∴
=
,
∴
=
,
∴BN=
,
作NH垂直BM于H,
∵∠B=45度,
∴NH=
BN=
,
∴S=
CM•NH
;
(2)令S△AMN=4,即4=
,
判别式b2-4ac<0,方程无解.
故不存在点M,使△AMN的面积等于4.

∵MN∥AC,
∴S△CMN=S△AMN,
∵CM=x,则BM=2
| 2 |
∴△BMN∽BCA,
∴
| BM |
| BC |
| BN |
| BA |
∴
2
| ||
2
|
| BN |
| 3 |
∴BN=
6
| ||
2
|
作NH垂直BM于H,
∵∠B=45度,
∴NH=
| ||
| 2 |
6
| ||
| 4 |
∴S=
| 1 |
| 2 |
6
| ||
| 8 |
(2)令S△AMN=4,即4=
6
| ||
| 8 |
判别式b2-4ac<0,方程无解.
故不存在点M,使△AMN的面积等于4.
点评:本题考查了相似三角形的判定、解直角三角形的有关知识、三角形的面积公式运用以及一元二次方程解的存在性问题,题目的综合性强,计算量大.

练习册系列答案
相关题目
 (2004•泰安)如图,在△ABC中,AB=AC,点E、D、F在边BC上,且∠BAD=∠CAD.BE=CF,则图中全等的三角形共有( )
(2004•泰安)如图,在△ABC中,AB=AC,点E、D、F在边BC上,且∠BAD=∠CAD.BE=CF,则图中全等的三角形共有( )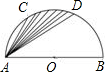 (2004•泰安)如图,点C、D是以AB为直径的半圆的三等分点,弧CD的长为
(2004•泰安)如图,点C、D是以AB为直径的半圆的三等分点,弧CD的长为 (2004•泰安)如图,AB是⊙O的弦,P是AB上一点,AB=10cm,PA:PB=2:3,OP=5cm,则⊙O的半径等于
(2004•泰安)如图,AB是⊙O的弦,P是AB上一点,AB=10cm,PA:PB=2:3,OP=5cm,则⊙O的半径等于 (2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.
(2004•泰安)如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.