题目内容
（2004•泰安）如图，在△ABC中，AB=AC，点E、D、F在边BC上，且∠BAD=∠CAD．BE=CF，则图中全等的三角形共有（ ）分析：根据等腰三角形三线合一的性质可得AD⊥BC，然后根据对称性找出全等的三角形即可得解．
解答：解：∵AB=AC，∠BAD=∠CAD，
∴AD⊥BC，
又∵BE=CF，
∴图形关于AD成轴对称，
∴全等的三角形有△ABE≌△ACF，△ABD≌△ACD，△ABF≌△ACE，△AED≌△AFD共4对．
故选C．
∴AD⊥BC，
又∵BE=CF，
∴图形关于AD成轴对称，
∴全等的三角形有△ABE≌△ACF，△ABD≌△ACD，△ABF≌△ACE，△AED≌△AFD共4对．
故选C．
点评：本题考查了全等三角形的判定，等腰三角形的性质，注意找出全等三角形时要按照一定的顺序，做到不重不漏．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
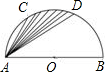（2004•泰安）如图，点C、D是以AB为直径的半圆的三等分点，弧CD的长为
（2004•泰安）如图，AB是⊙O的弦，P是AB上一点，AB=10cm，PA：PB=2：3，OP=5cm，则⊙O的半径等于
（2004•泰安）如图，在△ABC中，AB=3，BC=
（2004•泰安）如图，Rt△AOB的两直角边OA、OB的长分别是1和3，将△AOB绕O点按逆时针方向旋转90°，至△DOC的位置．