Question

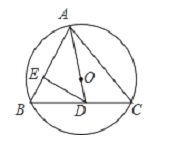
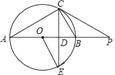
【题目】如图，已知，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点，连结OE，AC，且∠P=∠E，∠POE=2∠CAB．

（1）求证：CE⊥AB；

（2）求证：PC是⊙O的切线；

（3）若BD=2OD，且PB=9，求⊙O的半径长和tan∠P的值．

Answer 1

【答案】(1)证明见解析；（2）证明见解析；（3）

【解析】分析：（1）连结OC，如图，根据圆周角定理得∠POC=2∠CAB，由于∠POE=2∠CAB，则∠POC=∠POE，根据等腰三角形的性质即可得到CE⊥AB；

（2）由CE⊥AB得∠P+∠PCE=90°，加上∠E=∠OCD，∠P=∠E，所以∠OCD+∠PCE=90°，则OC⊥PC，然后根据切线的判定定理即可得到结论．

（3）设⊙O的半径为r，OD=x，则BD=2x，r=3x，易证得Rt△OCD∽Rt△OPC，根据相似三角形的性质得OC2=ODOP，即（3x）2=x（3x+9），解出x，即可得圆的半径；同理可得PC2=PDPO=（PB+BD）（PB+OB）=162，可计算出PC，然后在Rt△OCP中，根据正切的定义即可得到tan∠P的值．

详解：（1）证明：连接OC，

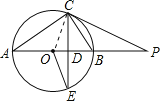
∴∠COB=2∠CAB，

又∠POE=2∠CAB．

∴∠COD=∠EOD，

又∵OC=OE，

∴∠ODC=∠ODE=90°，

即CE⊥AB；

（2）证明：∵CE⊥AB，∠P=∠E，

∴∠P+∠PCD=∠E+∠PCD=90°，

又∠OCD=∠E，

∴∠OCD+∠PCD=∠PCO=90°，

∴PC是⊙O的切线；

（3）解：设⊙O的半径为r，OD=x，则BD=2x，r=3x，

∵CD⊥OP，OC⊥PC，

∴Rt△OCD∽Rt△OPC，

∴OC2=ODOP，即（3x）2=x（3x+9），

解之得x=，

∴⊙O的半径r=，

同理可得PC2=PDPO=（PB+BD）（PB+OB）=162，

∴PC=9，

在Rt△OCP中，tan∠P=．