Question

【题目】已知抛物线 y＝x2+bx+与 y轴交于点 B，将该抛物线平移，使其经过点 A（-，0），且与 x轴交于另一点 C．若 b≤﹣2，则线段 OB，OC的大小关系是（ ）

A. OB≤OC B. OB＜OC C. OB≥OC D. OB＞OC

Answer 1

【答案】D

【解析】

由二次函数y＝x2+bx的图象上点的坐标特征求得点B的坐标，由顶点坐标公式求得点A的坐标，根据抛物线平移规律和待定系数法求平移后抛物线的解析式，易比较线段OB，OC的大小关系．

如下图所示：

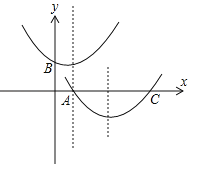
由y＝x2+bx（x）2+得到B（0，），故OB．

该抛物线的顶点坐标是（）．

设：抛物线向右平移了m个单位、下平移n个单位（m＞0，n＞0），平移后抛物线顶点坐标为（m，），则平移后抛物线的解析式为：y＝（xm）2n，（xC﹣xA）2＝（xC+xA）2﹣4xAxC＝4n﹣b2，xCOC，OB﹣OC．

∵b≤﹣2＜0，∴b+1≤﹣1＜0，∴OB﹣OC0，抛物线向左平移了m个单位、下平移n个单位（m＞0，n＞0），用同样的方法验证：OB＞OC．

故选D．