题目内容

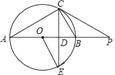
【题目】在Rt△ABC中，∠C=90°，cosB=0.6，把这个直角三角形绕顶点C旋转后得到Rt△A'B'C，其中点B'正好落在AB上，A'B'与AC相交于点D，那么B′D：CD=_____．

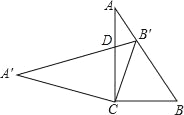
【答案】0.35

【解析】作CH⊥AB于H，先在Rt△ABC中，根据余弦的定义得到cosB==0.6=，设BC=3x，则AB=4x，再根据勾股定理计算出AC=4x，在Rt△HBC中，根据余弦的定义可计算出BH=x，接着根据旋转的性质得CA′=CA=4x，CB′=CB，∠A′=∠A，所以根据等腰三角形的性质有B′H=BH=x，则AB′=x，然后证明△ADB′∽△A′DC，再利用相似比可计算出B′D与DC的比值=0.35．

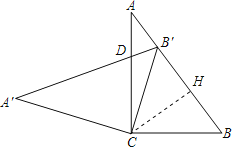
故答案为：0.35.

练习册系列答案
相关题目

【题目】如图一次函数的图象分别交x轴、y轴于点A,B，与反比例函数图象在第二象限交于点C(m，6)，轴于点D，OA＝OD．

（1）求m的值和一次函数的表达式；

（2）在X轴上求点P，使△CAP为等腰三角形（求出所有符合条件的点）

【题目】如图，已知，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点，连结OE，AC，且∠P=∠E，∠POE=2∠CAB．

（1）求证：CE⊥AB；

（2）求证：PC是⊙O的切线；

（3）若BD=2OD，且PB=9，求⊙O的半径长和tan∠P的值．

【题目】如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，则FM的长为 ．

【题目】当m是何值时，关于x的方程（m2+2）x2+（m﹣1）x﹣4=3x2

（1）是一元二次方程；

（2）是一元一次方程；

（3）若x=﹣2是它的一个根，求m的值．

【题目】已知正比例函数和反比例函数的图象都经过点 A（3，3）．

（1）求正比例函数和反比例函数的解析式；

（2）把直线 OA 向下平移后得到直线 l，与反比例函数的图象交于点 B（6，m），求 m 的值和直线 l 的解 析式；

（3）在（2）中的直线 l 与 x 轴、y 轴分别交于 C、D，求四边形 OABC 的面积．

【题目】在学习掷硬币的概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是”，小明做了下列三个模拟实验来验证．

①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值；

②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值；

③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥（如图），从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值． 上面的实验中，不科学的有（　　）

A. 0个 B. 1个 C. 2个 D. 3个

【题目】某公司在羊年春节晚会上举行一个游戏，规则如下：有4张背面相同的卡片，正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像，分别对应1000元、600元、400元、200元的奖金，现将4张纸牌洗匀后背面朝上摆放到桌上，让员工抽取，每人有两次抽奖机会，两次抽取的奖金之和作为公司发的年终奖金．现有两种抽取的方案：①小芳抽取方案是：直接从四张牌中抽取两张．②小明抽取的方案是：先从四张牌中抽取一张后放回去，再从四张中再抽取一张．你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大？请用树形图或列表法进行分析说明．

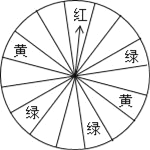
【题目】“六一”儿童节期间，某商厦为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准哪个区域，顾客就可以获得相应的奖品．

颜色

奖品

红色

玩具熊

黄色

童话书

绿色

彩笔

小明和妈妈购买了125元的商品，请你分析计算：

(1)小明获得奖品的概率是多少？

(2)小明获得童话书的概率是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网