题目内容
【题目】△ABC中,BC=12,高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)设EF=x,EH=y,写出y与x之间的函数表达式;
(3)设矩形EFGH的面积为S,求S与x之间的函数表达式,并写出S的最大值.

【答案】(1)见解析;(2)y=8﹣![]() x(0<x<12);(3)S矩形EFGH=﹣
x(0<x<12);(3)S矩形EFGH=﹣![]() (x﹣6)2+24,Smax=24.
(x﹣6)2+24,Smax=24.
【解析】
(1)先判断出AM是△AEF的高,再判断出△AEF∽△ABC,即可得出结论;(2)先判断出四边形EMDG是矩形,得出DM=EH,进而表示出AM=8﹣y,借助(1)的结论即可得出结论;(3)由矩形的面积公式得出函数关系式,即可得出结论.
解:(1)∵四边形EFGH是矩形,
∴EF∥BC,
∵AD是△ABC的高,
∴AD⊥BC,
∴AM⊥EF,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() (相似三角形的对应边上高的比等于相似比);
(相似三角形的对应边上高的比等于相似比);
(2)∵四边形EFGH是矩形,
∴∠FEH=∠EHG=90°,
∵AD⊥BC,
∴∠HDM=90°=∠FEH=∠EHG,
∴四边形EMDH是矩形,
∴DM=EH,
∵EF=x,EH=y,AD=8,
∴AM=AD﹣DM=AD﹣EH=8﹣y,
由(1)知,![]() ,
,
∴![]() ,
,
∴y=8﹣![]() x(0<x<12);
x(0<x<12);
(3)由(2)知,y=8﹣![]() x,
x,
∴S=S矩形EFGH=xy=x(8﹣![]() x)=﹣
x)=﹣![]() (x﹣6)2+24,
(x﹣6)2+24,
∵a=﹣![]() <0,
<0,
∴当x=6时,Smax=24.

【题目】为了满足广大手机用户的需求,某移动通信公司推出了三种套餐,资费标准如下表所示:
套餐资费标准 | |||||||
月套餐类型 | 套餐费用 | 套餐包含内容 | 超出套餐后的费用 | ||||
本地主叫市话 | 短信 | 国内移动数据流量 | 本地主叫市话 | 短信 | 国内移动数据流量 | ||
套餐一 | 18元 | 30分钟 | 100条 | 50兆 | 0.1元/ | 0.1元/条 | 0.5元/兆 |
套餐二 | 28元 | 50分钟 | 150条 | 100兆 | |||
套餐三 | 38元 | 80分钟 | 200条 | 200兆 | |||
小莹选择了该移动公司的一种套餐,下面两个统计图都反映了她的手机消费情况.
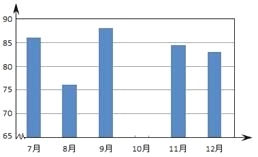
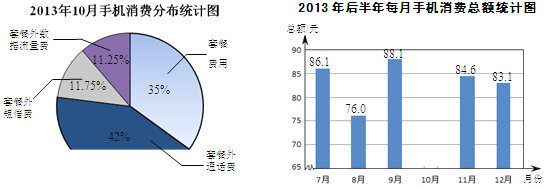
(1)已知小莹2013年10月套餐外通话费为33.6元,则她选择的上网套餐为________套餐(填“一”、“二”或“三”);
(2)补全条形统计图,并在图中标明相应的数据;
(3)根据2013年后半年每月的消费情况,小莹估计自己每月本地主叫市话通话大约430分钟,发短信大约240条,国内移动数据流量使用量大约为120兆,除此之外不再产生其他费用,则小莹应该选择________套餐最划算(填“一”、“二”或“三”);选择该套餐后,她每月的手机消费总额约为________元.