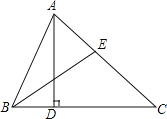
��Ŀ����
����Ŀ����ͼ�٣���֪������C1��y=a��x+1��2��4�Ķ���ΪC����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����B�ĺ�������1��
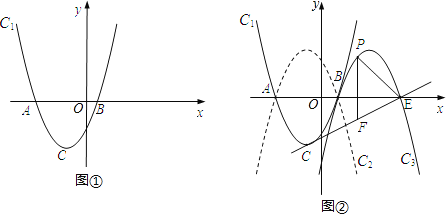
��1�����C�����꼰a ��ֵ��
��2����ͼ�ڣ�������C2��C1����x��Գƣ���������C2����ƽ��4����λ���õ�������C3��C3��x�ύ�ڵ�B��E����P��ֱ��CE�Ϸ�������C3�ϵ�һ�����㣬����P��y���ƽ���ߣ���CE�ڵ�F��
�����߶�PF�������ֵ��
����PE=EF�����P�����꣮
���𰸡���1��a=1������CΪ����1����4������2���ٵ�x=![]() ʱ��PF�����ֵΪ
ʱ��PF�����ֵΪ![]() ����P��
����P��![]() ��
��![]() ����
����
��������
�����������1�����ݶ��κ��������ʼ���ֱ����ö���C�����꣬��B��������뺯������ʽ�������a��ֵ��
��2����C2�Ķ���������C����x��ĶԳƵ㣬�Ҷ�����ϵ����Ϊ�෴�����ݴ˼������C2�Ľ���ʽ��Ȼ�����ƽ�Ƶ��������C3�Ľ���ʽ�����ô���ϵ�������ֱ��CE�Ľ���ʽ����PF�ij���������x��ʾ������Ȼ����ݶ��κ������������PF�����ֵ��
��PE=EF��P��F����x��Գƣ��������껥Ϊ�෴�����ݴ˼����з�����⣮
�⣺��1������CΪ����1����4����
����B��1��0����������C1�ϣ���0=a��1+1��2��4����ã�a=1��
��2������C2��C1����x��Գƣ�
��������C2�ı���ʽΪy=����x+1��2+4��
������C3��C2ƽ�Ƶõ���
��������C3Ϊy=����x��3��2+4=��x2+6x��5��
��E��5��0����
��ֱ��CE�Ľ���ʽΪ��y=kx+b��
��![]() �����
�����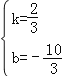 ��
��
��ֱ��BC�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��P��x����x2+6x��5������F��x��![]() x��
x��![]() ����
����
��PF=����x2+6x��5������![]() x��
x��![]() ��=��x2+
��=��x2+![]() x��
x��![]() =����x��
=����x��![]() ��2+
��2+![]() ��
��
����x=![]() ʱ��PF�����ֵΪ
ʱ��PF�����ֵΪ![]() ��
��
����PE=EF����PF��x�ᣬ
��x��ƽ��PF��
����x2+6x��5=��![]() x+
x+![]() ��
��
���x1=![]() ��x2=5����ȥ��
��x2=5����ȥ��
��P��![]() ��
��![]() ����
����

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�