题目内容
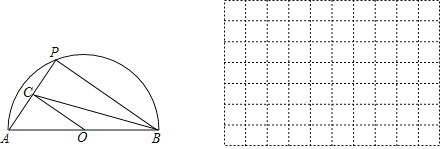
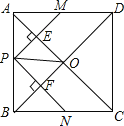
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
A.5个 B.4个 C.3个 D.2个
【答案】B
【解析】
试题∵四边形ABCD是正方形,∴∠BAC=∠DAC=45°。
∵在△APE和△AME中, ,
,
∴△APE≌△AME。故①正确。
∴PE=EM=![]() PM。
PM。
同理,FP=FN=![]() NP。
NP。
∵正方形ABCD中AC⊥BD,又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE。
∴四边形PEOF是矩形。∴PF=OE。∴PE+PF=OA。
又∵PE=EM=![]() PM,FP=FN=
PM,FP=FN=![]() NP,OA=
NP,OA=![]() AC,∴PM+PN=AC。故②正确。
AC,∴PM+PN=AC。故②正确。
∵四边形PEOF是矩形,∴PE=OF。
在直角△OPF中,OF2+PF2=PO2,∴PE2+PF2=PO2。故③正确。
∵△BNF是等腰直角三角形,而△POF不一定是。故④错误;
∵△AMP是等腰直角三角形,当△PMN∽△AMP时,△PMN是等腰直角三角形,
∴PM=PN。
又∵△AMP和△BPN都是等腰直角三角形,∴AP=BP,即P时AB的中点。故⑤正确。
综上所述,正确的结论有①②③⑤四个。故选B。

 寒假学与练系列答案
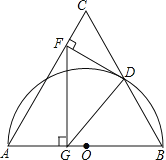
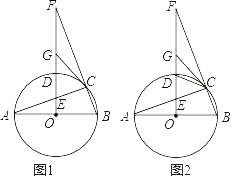
寒假学与练系列答案【题目】如图,P是半圆弧![]() 上一动点,连接PA、PB,过圆心O作
上一动点,连接PA、PB,过圆心O作![]() 交PA于点C,连接
交PA于点C,连接![]() 已知
已知![]() ,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
![]() 说明:补全表格时相关数据保留一位小数
说明:补全表格时相关数据保留一位小数![]()
![]() 建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:直接写出
结合画出的函数图象,解决问题:直接写出![]() 周长C的取值范围是______.
周长C的取值范围是______.