Question

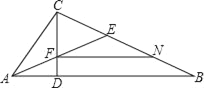
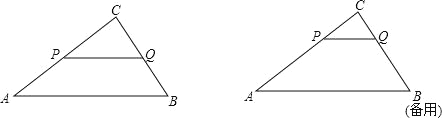
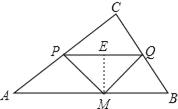
【题目】如图：已知△ABC中，AB＝5，BC＝3，AC＝4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．

（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；

（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；

（3）试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长．

Answer 1

【答案】（1） ；（2） ；（3）存在，和.

【解析】

（1）由于PQ∥AB，故△PQC∽△ABC，当△PQC的面积与四边形PABQ的面积相等时，△CPQ与△CAB的面积比为1：2，根据相似三角形的面积比等于相似比的平方，可求出CP的长；

（2）由于△PQC∽△ABC，根据相似三角形的性质，可用CP表示出PQ和CQ的长，进而可表示出AP、BQ的长．根据△CPQ和四边形ABQP的周长相等，可将相关的各边相加，即可求出CP的长；

（3）因为不能确定哪个角是直角，故应分类讨论．

①当∠MPQ＝90°，且PM＝PQ时．因为△CPQ∽△CAB，根据相似三角形边长的比等于高的比，可求出PQ的值；

②∠PQM＝90°时与①相同；

③当∠PMQ＝90°，且PM＝MQ时，过M作ME⊥PQ，则ME＝PQ，根据相似三角形边长的比等于高的比，可求出PQ的值．

（1）∵PQ∥AB，

∴△PQC∽△ABC，

∵S△PQC＝S四边形PABQ，

∴S△PQC：S△ABC＝1：2，

∴，

∴CP＝CA＝2；

（2）∵△PQC∽△ABC，

∴，

∴，

∴CQ＝CP，

同理：PQ＝CP，

∴l△PCQ＝CP+PQ+CQ＝CP+CP+CP＝3CP，

I四边形PABQ＝PA+AB+BQ+PQ，

＝4﹣CP+AB+3﹣CQ+PQ，

＝4﹣CP+5+3﹣CP+CP，

＝12﹣CP，

∴12﹣CP＝3CP，

∴CP＝12，

∴CP＝；

（3）∵AC＝4，AB＝5，BC＝3，

∴△ABC中AB边上的高为，

①当∠MPQ＝90°，且PM＝PQ时，

∵△CPQ∽△CAB，

∴，

∴，

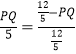∴PQ＝；

②当∠PQM＝90°时与①相同；

③当∠PMQ＝90°，且PM＝MQ时，

过M作ME⊥PQ，则ME＝PQ，

∴△CPQ的高为﹣ME＝﹣PQ，

∴，

∴，

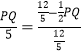∴PQ＝．

综合①②③可知：点M存在，PQ的长为或．