题目内容
【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
【答案】
(1)证明:∵∠BAC的角平分线AD,
∴∠BAE=∠CAD,
∵∠ABC=∠ADC,
∴△ABE∽△ADC
(2)证明:∵∠BAD=∠CAD,
∴ ![]() ,
,
∵OD为半径,
∴DO⊥BC(垂径定理),
∵F为OD的中点,
∴OB=BD,OC=CD,
∵OB=OC,
∴OB=BD=CD=OC,
∴四边形OBDC是菱形.

【解析】(1)根据圆周角定理求出∠B=∠D,根据相似三角形的判定推出即可;(2)根据垂径定理求出OD⊥BC,根据线段垂直平分线性质得出OB=BD,OC=CD,根据菱形的判定推出即可.
【考点精析】掌握菱形的判定方法和圆周角定理是解答本题的根本,需要知道任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: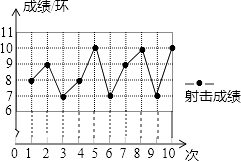
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.





