��Ŀ����
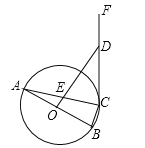
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��y�ύ�ڵ�A����x�ύ�ڵ�B���ҡ�BAO=30�㣬�ֽ���OAB��ֱ��AB���ۣ��õ���CAB. ����OC��AB�ڵ�D.
��1����֤��AD��OC��OD��![]() OA ��
OA ��
��2����Rt��AOB��б��AB��![]() ����OB��_____��OA��_____����C������Ϊ_______��
����OB��_____��OA��_____����C������Ϊ_______��
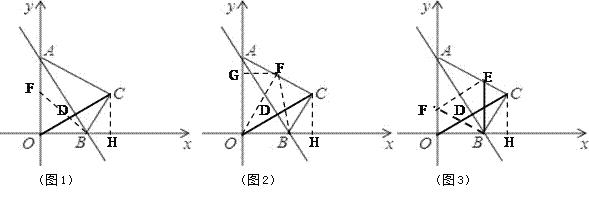
��3���ڣ�2���������£�����F�ӵ�O��������2����λ����/����ٶ�������O��A��C���յ�C�˶�������FOB�����ΪS��S��0������F���˶�ʱ��Ϊt�룬��S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
��4���ڣ�3���������£�����B��BE��x�ᣬ��AC�ڵ�E���ڶ���F���˶������У���tΪ��ֵʱ����BEF����BEΪ���ĵ��������Σ�

���𰸡� (1)�������� ��2��![]() ,6, ��
,6, ��![]() ��3�� (3)
��3�� (3) 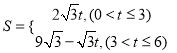 ;(4) ��t��1��3ʱ����BEF����BEΪ���ĵ���������.
;(4) ��t��1��3ʱ����BEF����BEΪ���ĵ���������.
�������������������1�������۵������ʺ͵ȱ������ε��ж��õ���OAC�ǵȱ������Σ���ϵȱ������εġ����ߺ�һ��������֤�ý��ۣ�
��2����ͼ1����C����CH��x����H�㣬��ֱ�ǡ�OCH�У��������Ǻ������CH��OH����C�����꼴����ã�
��3���ֳɵ�0��t��3��3��t��6������������������ε������ʽ������⣻
��4���ֳ�B�Ƕ��Ƕ����E�Ƕ��Ƕ�����������������ۣ�
���������
��1�����۵������ʵã� CA��OA�� CB��OB����BAC����BAO��30������ACB����AOB��90����
�� ��ABC����ABO=60����
�� ��OAC�ǵȱ�������
��OC��OA ��
�� ��DAC=��DAO ��
�� AD��OC��OD��![]() OC ��
OC ��
�� AD��OC��OD��![]() OA ��
OA ��
��2�� OB��![]() �� OA��6�� C��
�� OA��6�� C��![]() ��3����
��3����
��3��������������ۣ�
�ٵ�0��t��3ʱ����ͼ1�� OF��2t�� ![]() ��
��
�ڵ�3��t��6ʱ����ͼ2�� AF��2t��6�� ����F��FG��OA��G��
�� ![]() �� OG��OA�� AG��6����t��3����9��t��
�� OG��OA�� AG��6����t��3����9��t��
![]() ��
��
���������� 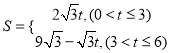
��4��������������ۣ�
�� ����BE��BFʱ�� ��ͼ3��
��BE��OA ��
���ABE����OAB��30�� ��
���EBA����EAB��30�� ��
��BE��AE ����EBC��60����30����30�� ��
����Rt��BOF��Rt��BCE����BF��BE ��BO��BC ��
����BOF�ա�BCE����HL��
��OF��CE �� ��FBO����EBC��30�� ��
����EBF��120����30����30��60�� ��
�� ��ʱ��BEFΪ�ȱ������Σ�BF=AF��
��Rt��FBO ���� ��FBO��30��
�� FO��![]() BF��
BF��![]() AF��
AF��
��AF��2 FO��
��AO��3FO��
��3FO��6��
�� FO��2 ��
�� 2t��2��
����ʱt��1��
�ڵ���BE��FEʱ�����Ͽ�֪����Fʹ����BEFΪ�ȱ������� �� ��F�˶���A���غϣ�
�� 2t��2������ 2t��6��
�� ��ʱ t��1���� t��3����
������������t��1��3ʱ����BEF����BEΪ���ĵ��������Σ�