题目内容
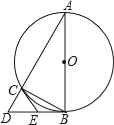
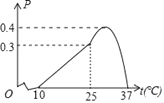
【题目】某农作物的生长率p与温度t(℃)有如下关系:如图,当10≤t≤25时可近似用函数p=![]() t﹣
t﹣![]() 刻画;当25≤t≤37时可近似用函数p=﹣
刻画;当25≤t≤37时可近似用函数p=﹣![]() (t﹣h)2+0.4刻画.
(t﹣h)2+0.4刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率p之间满足已学过的函数关系,部分数据如下:
生长率p | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
求:①m关于p的函数表达式;
②用含t的代数式表示m.
③天气寒冷,大棚加温可改变农作物生长速度.大棚恒温20℃时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天,但若欲加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:农作物上市售出后大棚暂停使用)
【答案】(1)29;(2)①m=100p﹣20;②m=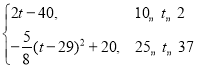 ;③29,理由见解析.
;③29,理由见解析.
【解析】
(1)把(25,0.3)代入p=﹣![]() (t﹣h)2+0.4中,便可求得h;
(t﹣h)2+0.4中,便可求得h;
(2)①由表格可知,m是p的一次函数,由待定系数法可解;
②分别求出当10≤t≤25时和当25≤t≤37时的函数解析式即可;
③分别求出当20≤t≤25时,增加的利润和当25<t≤37时,增加的利润,然后比较两种情况下的最大值,即可得结论.
解:(1)把(25,0.3)代入p=﹣![]() (t﹣h)2+0.4得:0.3=﹣
(t﹣h)2+0.4得:0.3=﹣![]() (25﹣h)2+0.4,
(25﹣h)2+0.4,
解得:h=29或h=21,
∵25≤t≤37
∴h=29.
(2)①由表格可知,m是p的一次函数,
设m=kp+b,
把(0.2,0),(0.3,10)代入得![]()
解得![]()
∴m=100p﹣20.
②当10≤t≤25时,p=![]() t﹣
t﹣![]() ,
,
∴m=100(![]() t﹣
t﹣![]() )﹣20=2t﹣40;
)﹣20=2t﹣40;
当25≤t≤37时,p=﹣![]() (t﹣h)2+0.4
(t﹣h)2+0.4
∴m=100[﹣![]() (t﹣h)2+0.4]﹣20=
(t﹣h)2+0.4]﹣20=![]() (t﹣29)2+20,
(t﹣29)2+20,
∴m=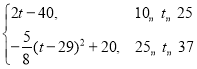
③当20≤t≤25时,增加的利润为:
600m+[100×30﹣200(30﹣m)]=800m﹣3000=1600t﹣35000,
当t=25时,增加的利润的最大值为1600×25﹣35000=5000元;
当25<t≤37时,增加的利润为:
600m+[100×30﹣400(30﹣m)]=1000m﹣9000=﹣625(t﹣29)2+11000
∴当t=29时,增加的利润的最大值为11000元.
综上,当t=29时,提前20天上市,增加的利润最大,最大值为11000元.

 阅读快车系列答案
阅读快车系列答案【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
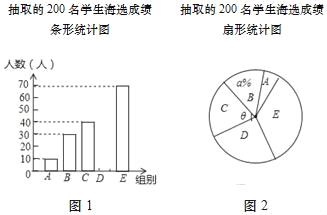
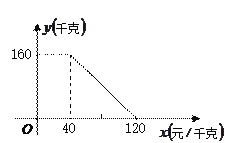
【题目】《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x≤100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
(4)经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?