题目内容
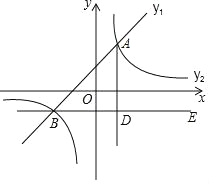
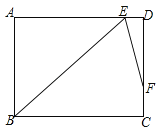
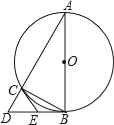
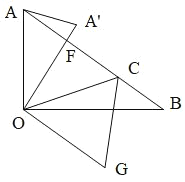
【题目】如图,在 Rt△AOB 中,∠AOB=90°,OA=3,OB=4,线段 OA’绕点 O 顺时针旋转ɑ角(0≤ɑ≤180°),OA’交边 AB 于点 F.
(1)当旋转ɑ角度后,A’点恰好落在 AB 上,记为 C 点,求 CB 的长度;
(2)当 OA’绕点 O 旋转与 AB 平行时,记为 OG,连接 CG,交 OB 于 E,分别求出 OE 长度和∠COB 的正弦值;
(3)在旋转过程中,请直接写出![]() 的最大值.
的最大值.
【答案】(1)CB=![]() ;(2)OE=
;(2)OE=![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1) 过O作AB的垂线交AB于D,根据面积法求出AD,从而可求出CB;
(2)平行得△CEB![]() △OEG, 过C作CH⊥OB,可求
△OEG, 过C作CH⊥OB,可求![]() 长度和∠
长度和∠![]() 的正弦值;
的正弦值;
(3)由图像易知当OA'⊥AB时,FO最短,此时![]() 取得最大值为
取得最大值为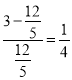
解:(1) 过O作AB的垂线交AB于D,
∵![]() ,
,
∴OD=![]() ,
,
∴AD=CD=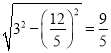 ,
,
CB=![]() ;
;
(2)∵OG∥AB,
∴∠B=∠BOG,
∵∠BEC=∠OEG,
∴以△CEB∽△GEO,
∴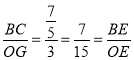 ,
,
∴BE=![]() ,
,
∵OB=EB+EO=4,
∴OE+![]() =4,
=4,
解得OE=![]() ,
,
过C作CH⊥OB,则△BCH∽△BAO,
∴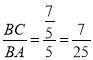 =
=![]() ,
,
∴CH=![]()
![]() ,
,
∴ ;
;
(3)由图像易知当OA'⊥AB时,FO最短,此时![]() 取得最大值为
取得最大值为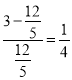 .
.

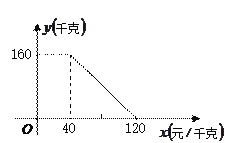
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值