题目内容
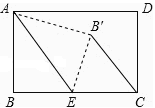
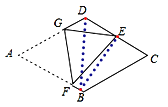
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析: 连接BE,BD,如图,利用菱形的性质得△BDC为等边三角形,在Rt△BCE中计算出BE=![]() ,接着证明BE⊥AB, 利用折叠的性质得到EF=AF.,设EF=AF=x, FG垂直平分AE,所以在Rt△BEF中利用勾股定理列方程求解即可.
,接着证明BE⊥AB, 利用折叠的性质得到EF=AF.,设EF=AF=x, FG垂直平分AE,所以在Rt△BEF中利用勾股定理列方程求解即可.
详解: 连接BE,BD,如图,
∵四边形ABCD为菱形,∠A=60°,
∴△BDC为等边三角形, ∠C=∠A=60°,
∴∠CBE=90°-60°=30°.
∵E点为CD的中点,
∴CE=DE=1,BE⊥CD.
在Rt△BCE中,
BC=2CE=2,
BE=![]() .
.
∵AB∥CD,
∴BE⊥AB.
∵菱形纸片翻折,使点A落在CD的中点E处,
∴EF=AF.
设EF=AF=x,则BF=2-x,
在Rt△BEF中,
![]() ,
,
解得![]() .
.
故选A.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目